Предмет: Алгебра,
автор: unicorn2837
При каких значениях параметра а произведение корней уравнения x^2+(a+1)x+a²-3a=0 равно 4?
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!!
Решите с подробным объяснением
Приложения:
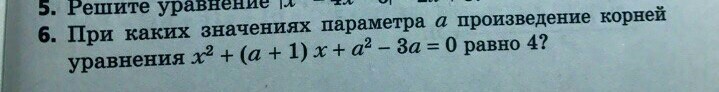
Аноним:
a^2-3a-4=0
a=4
Ответы
Автор ответа:
15
-1 не удовлетворяет первому неравенству, поэтому ответ 4
СПАСИБО ОГРОМНОЕ!!!!!!)
пожалуйста)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: arinakireeva61
Предмет: Физика,
автор: 1a1a34
Предмет: Физика,
автор: Viktoria0955
Предмет: Физика,
автор: milanyamuzafar