Предмет: Математика,
автор: anplex770
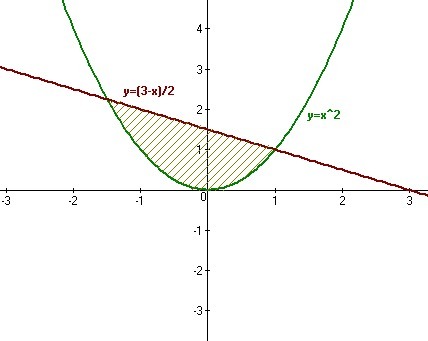
Найти площадь фигуры, ограниченной линиями.
y=x^2, x+2y-3=0
Ответы
Автор ответа:
1
Приложения:
anplex770:
Большое спасибо!
Похожие вопросы
Предмет: Математика,
автор: LOLOVA000
Предмет: Обществознание,
автор: aizara130512
Предмет: География,
автор: ivkevychnatali
Предмет: Математика,
автор: Аноним