Предмет: Математика,
автор: eunartova
СРОЧНООО ПОМОГИТЕ!!
Доведите , что при любом натуральном значении n , это будет делиться на 10
Приложения:
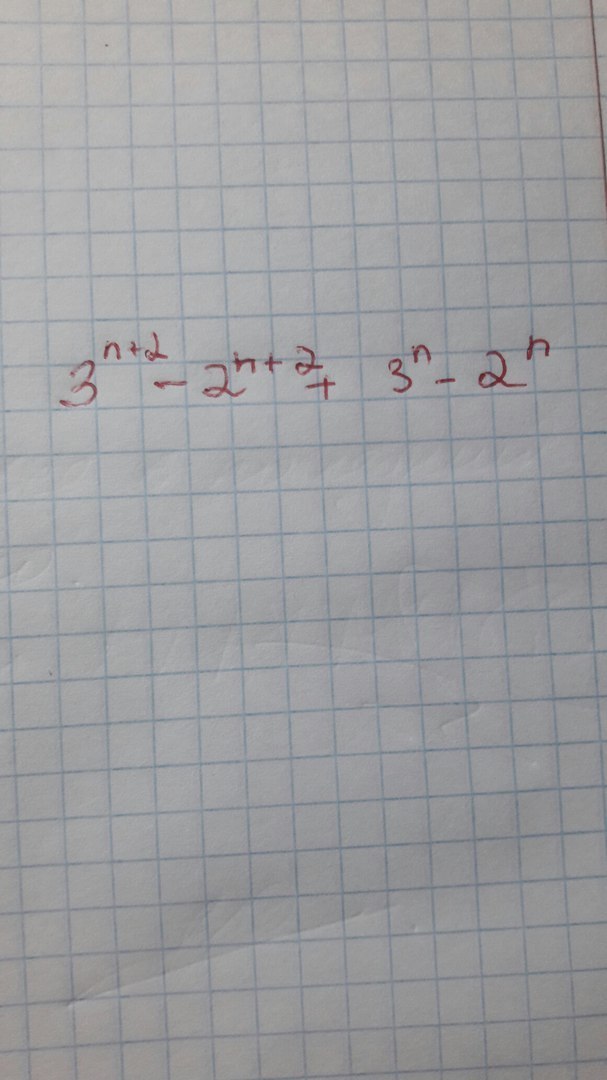
AlfaAndOmega:
именно на 10?
да
Ответы
Автор ответа:
1
Представим 3^(2+n) как (3^n)*(3^2)
Представим 2^(2+n) как (2^n)*(2^2)
Получим (3^n)*(3^2) - (2^n)*(2^2) + (3^n) - (2^n) вынесем за скобки 3^n и (-2^n)
(3^n)(3^2+1) - 2^n(2^2+1) = (3^n)(10) - (2^n)(5)=10*3^n-5*2^n=5(2*3^n-2^n)
Представим 2^n как 2*2^(n-1)
5(2*3^n-2*2^(n-1)) выносим за скобки 2
10(3^n-2^(n-1))
Произведение делится на 10
Представим 2^(2+n) как (2^n)*(2^2)
Получим (3^n)*(3^2) - (2^n)*(2^2) + (3^n) - (2^n) вынесем за скобки 3^n и (-2^n)
(3^n)(3^2+1) - 2^n(2^2+1) = (3^n)(10) - (2^n)(5)=10*3^n-5*2^n=5(2*3^n-2^n)
Представим 2^n как 2*2^(n-1)
5(2*3^n-2*2^(n-1)) выносим за скобки 2
10(3^n-2^(n-1))
Произведение делится на 10
если что спрашивай
Похожие вопросы
Предмет: Физика,
автор: foxconn23
Предмет: Математика,
автор: kirinfg
Предмет: Биология,
автор: SANO65806
Предмет: Биология,
автор: renatayus18