Question

Площадь поверхности фигуры, склеенной из одинаковых кубиков с ребром 1 см, соединенных гранями так, что совпадают вершины склеенных граней, равна 30 . Сколько кубиков было использовано?

Answer 1

РЕШЕНИЕ
Попробуем найти формулу зависимости площади и числа кубиков.
n = 1,  S1 =6
n = 2, S2 = 10 = 2*6 - 2 - две грани вместе склеены - стало меньше.
n = 3, S3 = 14 = 3*6 - 4
Формула площади в общем виде 
Sn = n*6 - 2*(n-1) = 4*n +2 - число граней.
Или обратная формула числа кубиков
n = (S - 2)/4
В нашей задаче S = 30.
Находим число кубиков.
n = (30-2)/4 = 28/4 = 7 штук - ОТВЕТ
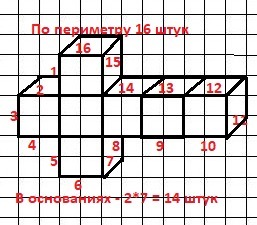
Вариант фигуры из семи кубиков на рисунке в приложении.
Проверка.
Площадь оснований - 2*7 = 14 граней.
Площадь по периметру - 16 граней.
ИТОГО = 14+16 = 30 граней - правильно.

Answer 2

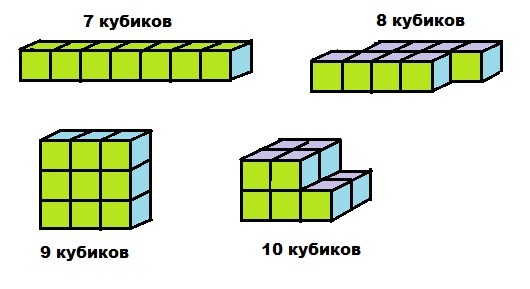
Задача имеет несколько решений
1. 7 кубиков склеены в ряд.
   Площадь поверхности  7*4 + 2*1 = 30 см²
2. 8 кубиков склеены в два ряда со сдвигом
   Площадь поверхности 5*2 + 8*2 + 2*2 = 30 см²
3. 9 кубиков склеены в прямоугольный параллелепипед
  Площадь поверхности  9*2 + 3*4 = 30 см²
4. 10 кубиков склеены ступенькой
  Площадь поверхности 5*2 + 6*2 + 4*2 = 30 см²