Предмет: Математика,
автор: ПрофиЗнания
Исследовать сходимости рядов.3 нужен
Приложения:
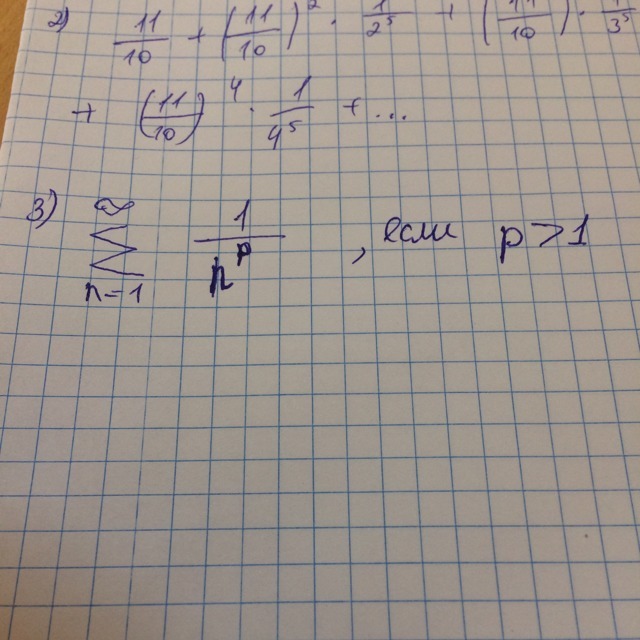
Ответы
Автор ответа:
0
Исследовать сходимости ряд  , где р > 1.
, где р > 1.
Решение.
Вообще-то это гармонически ряд и при р > 1 - данный ряд сходится.
Это элементарные факты из теории рядов, которые уже доказаны, и при решении примера можно смело на это ссылаться.
Однако, давайте докажем сходимость ряда.
Для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю, тогда

Необходимое условие сходимости выполнено, однако для исследования ряда применим интегральный признак Коши. Рассмотрим функцию

функция непрерывна, монотонно убывает на промежутке![[1 \ ; \ + \infty ] [1 \ ; \ + \infty ]](https://tex.z-dn.net/?f=%5B1+%5C+%3B+%5C+%2B+%5Cinfty+%5D)


Отсюда видно, что при р>1 несобственный интеграл равен конечному числу, т.е. сходится, а значит и ряд тоже сходится!
Решение.
Вообще-то это гармонически ряд и при р > 1 - данный ряд сходится.
Это элементарные факты из теории рядов, которые уже доказаны, и при решении примера можно смело на это ссылаться.
Однако, давайте докажем сходимость ряда.
Для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю, тогда
Необходимое условие сходимости выполнено, однако для исследования ряда применим интегральный признак Коши. Рассмотрим функцию
функция непрерывна, монотонно убывает на промежутке
Отсюда видно, что при р>1 несобственный интеграл равен конечному числу, т.е. сходится, а значит и ряд тоже сходится!
Похожие вопросы
Предмет: Геометрия,
автор: lajksuper945
Предмет: Английский язык,
автор: oxishu15
Предмет: Алгебра,
автор: tt1tt1tt1rr
Предмет: Математика,
автор: evgeniiabondar
Предмет: Обществознание,
автор: Belbellita72