Предмет: Геометрия,
автор: MelissaKus
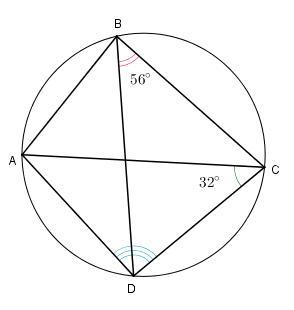
Чему равен угол ADC четырёхугольника ABCD, вписанного в
окружность, если угол ACD=32°, угол CBD = 56° ?
Ответы
Автор ответа:
14
Ответ: 92°.
Объяснение:
Вписанный угол равен половине дуги, на которую он опирается (свойство вписанных углов).
∪CD = 2 · ∠CBD = 2 · 56° = 112°
∪AD = 2 · ∠ACD = 2 · 32° = 64°
Градусная мера меньшей дуги АС: ∪AC = ∪AD + ∪CD = 112° + 64° = 176°.
Градусная мера большей дуги АС: ∪AC = 360° - 176° = 184°
∠ADC = 0.5 · ∪AC = 0.5 · 184° = 92°.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: vladislavovna911
Предмет: Математика,
автор: aidanaamirbekova8
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Mange11