Предмет: Математика,
автор: Аноним
Вычислите двойной интеграл .8 Задание прикрепила. Помогите чем можете❤️ дам 100 баллов)
Приложения:

Аноним:
спасибо
А где область?
Условие неполное
область задана прямой и параболой, то что между ними... (насколько я понял)
Ну тогда суть не меняет)
У меня решено )
выкладывай, автор просит на фотке..
у меня фоткать всё равно нечем
да)
Обновил фотку
Ответы
Автор ответа:
2
Приложения:
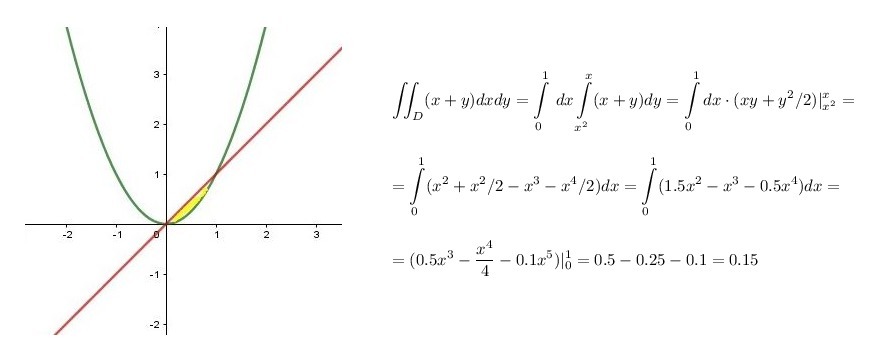
Нашел ошибочку
А не
dc` e Dfc ghfdbkmyj htityj
ой, всё у Вас правильно решено
только расписать стоило, как пределы интегрирования нашли..
в смысле по х ))
Заходим в график и выходим)
Автор ответа:
1
чисто что бы было, как альтернатива.
область интегрирования задана неявно.
изобразив график (примерно) видно, что точки (0;0) и (1;1) являются левой нижней и правой верхней, из чего
D={0<=x<=1; x²<=y<=x}={0<=y<=1;y<=x<=√y}


область интегрирования задана неявно.
изобразив график (примерно) видно, что точки (0;0) и (1;1) являются левой нижней и правой верхней, из чего
D={0<=x<=1; x²<=y<=x}={0<=y<=1;y<=x<=√y}
Похожие вопросы
Предмет: Алгебра,
автор: satovadara4
Предмет: Английский язык,
автор: besshtennovnik
Предмет: Математика,
автор: hladkovser
Предмет: Математика,
автор: Андрекш
Предмет: Математика,
автор: ксения562