Предмет: Математика,
автор: ПрофиЗнания
Исследовать сходимость , абсолютную сходимость и расходимость.
ДАЮ 100 БАЛЛОВ! СРОЧНА!!!
Приложения:
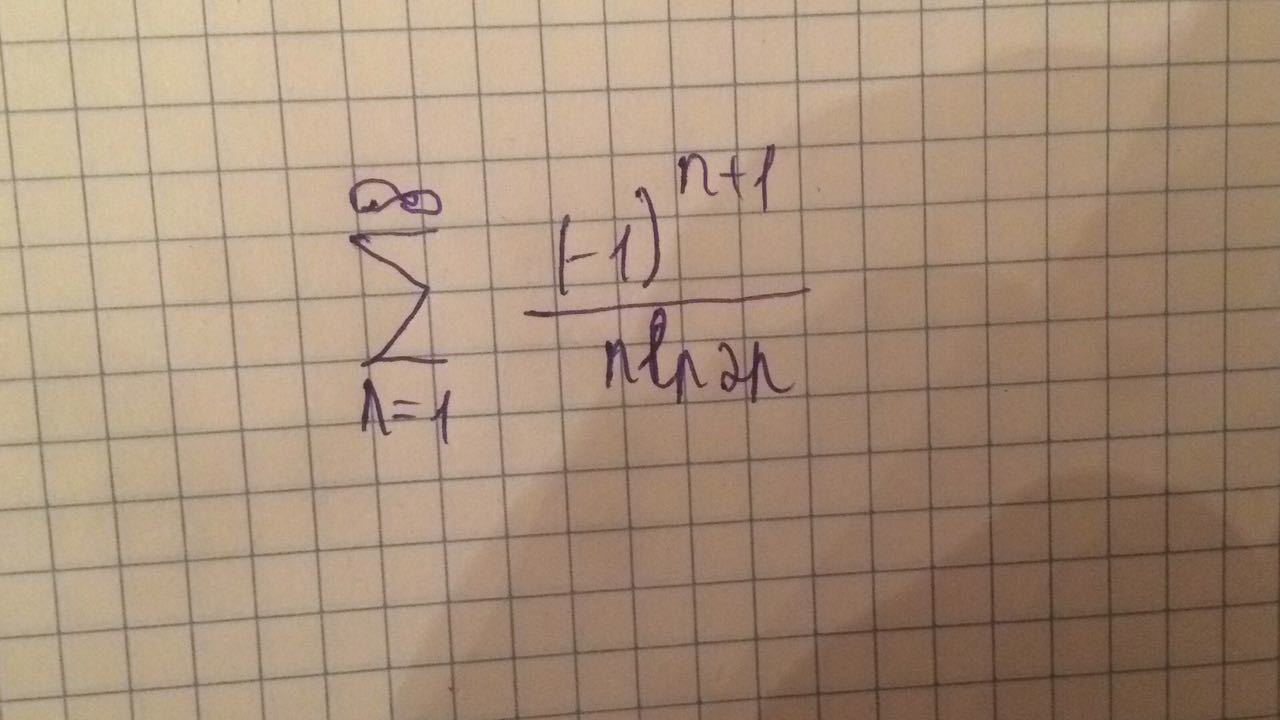
Аноним:
ln(2n)?
да
с ходу скажу, что сходится условно
Ествественно
я прокомментирую и поддержу решение Гаутер, схема решения : Лейбниц, - Коши (интегральный)
По интегральному признаку ряд расходится а по Лейбница сходится
во! решение в студию!!
https://znanija.com/task/28419645
Ответы
Автор ответа:
2
Первое условие признака Лейбница выполняется 1/ln2 > 1/ln8 > 1/ln216
 Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится.
Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится.
Исследуем теперь ряд на абсолютность. Возьмём ряд по модулю
 Применим интегральный признак:
Применим интегральный признак:
 Несобственный интеграл расходится, следовательно и ряд по модулю тоже расходится, а значит данный ряд будет сходится УСЛОВНО
Несобственный интеграл расходится, следовательно и ряд по модулю тоже расходится, а значит данный ряд будет сходится УСЛОВНО
Исследуем теперь ряд на абсолютность. Возьмём ряд по модулю
https://znanija.com/task/28419645
Похожие вопросы
Предмет: Физика,
автор: shisofrenik2006
Предмет: Биология,
автор: 1zB0rnotizzz
Предмет: Биология,
автор: karpinskajulia2009
Предмет: Обществознание,
автор: Last123
Предмет: Алгебра,
автор: Котэ200