Предмет: Математика,
автор: ПрофиЗнания
Исследовать сходимость , абсолютную сходимость и расходимость.
ДАЮ 100 БАЛЛОВ! СРОЧНА!!!
Приложения:
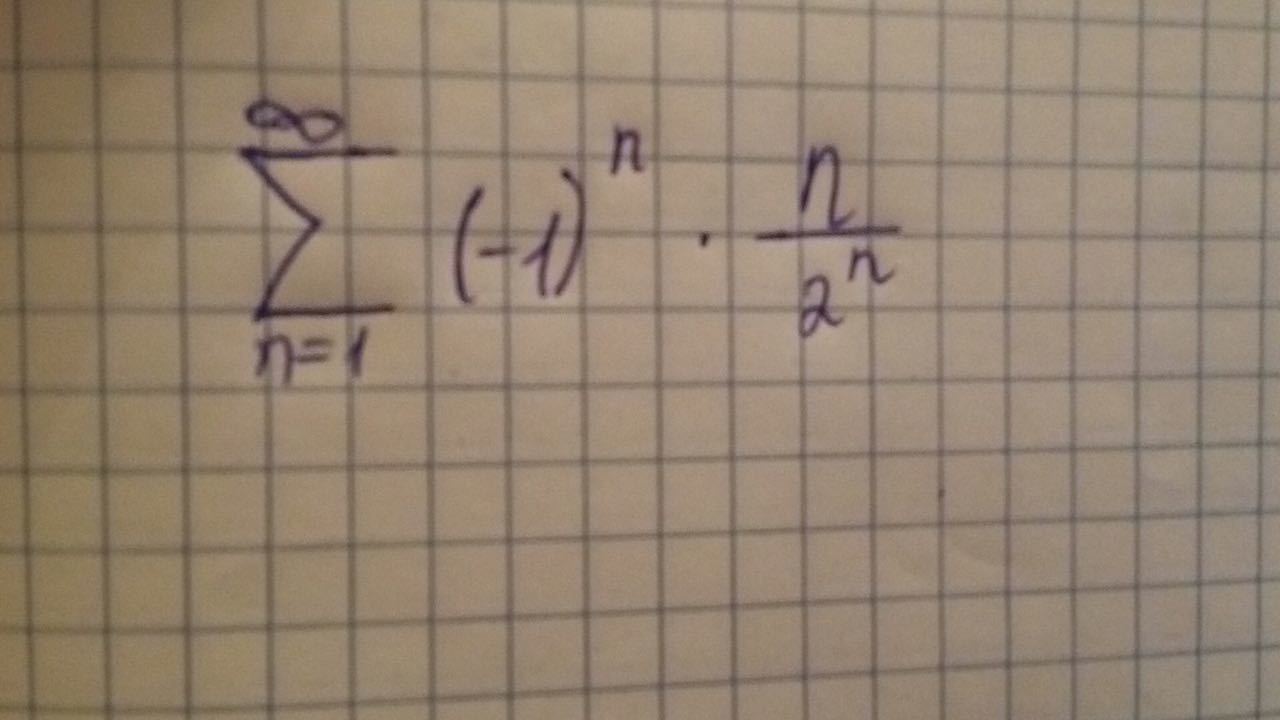
Ответы
Автор ответа:
1
Если подставить n=2 и n=3 то получим что 1/2 > 3/8. По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
Второе условие: . Второе условие Лейбница выполняется, значит данный ряд сходится.
. Второе условие Лейбница выполняется, значит данный ряд сходится.
Осталось теперь исследовать на абсолютную сходимость.
 - сходится.
- сходится.
Данный ряд будет сходится АБСОЛЮТНО
Второе условие:
Осталось теперь исследовать на абсолютную сходимость.
Данный ряд будет сходится АБСОЛЮТНО
pavlikleon:
уменьшение величины должно происходить начиная с некоторого члена ряда. Например если к имеющимуся ряду впереди пририсовать, что то имеющее конечную величину, общая сходимость ряда не изменится..
Если вы при n=1 хотите, то по модулю и так 1/2. А так решение было исправлено
увидел исправление, за свое высказывание первое, извините
Во-вторых, признак Лейбница - не дает гарантии абсолютной сходимости, абсолютную или условную сходимость проверяют другими методами
Естественно, еще дорабатываю
Я сейчас выставлю ещё одно за 98 баллов решите!
Автор ответа:
0
Рассмотрим ряд составленный из модулей, т.е. :
∑
Применим признак Даламбера:

И сравним q с 1

Получили q<1, значит ряд составленнный из модулей сходится,
что в свою очередь означает, что заданный знакочередующийся ряд СХОДИТСЯ АБСОЛЮТНО
∑
Применим признак Даламбера:
И сравним q с 1
Получили q<1, значит ряд составленнный из модулей сходится,
что в свою очередь означает, что заданный знакочередующийся ряд СХОДИТСЯ АБСОЛЮТНО
а где у вас (-1)^n
??
а мы сразу ряд из модулей рассматриваем, если он сходится, значит и знакочередующийся ряд сходится, притом сходится абсолютно
Я сейчас выставлю ещё одно за 98 баллов решите!
В добавку из абсолютной сходимости следует сходимость
https://znanija.com/task/28419645
реши пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: krnaxwn
Предмет: История,
автор: timohinalesa31
Предмет: Физкультура и спорт,
автор: abdubosidovumid
Предмет: Физика,
автор: Юлич1111
Предмет: Математика,
автор: Аноним