Предмет: Геометрия,
автор: Лулу52807
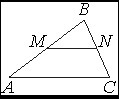
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=16, MN=12. Площадь треугольника ABC равна 80. Найдите площадь треугольника MBN.
Объясните подробно, пожалуйста! Рисунок прикрепила.
Приложения:
Ответы
Автор ответа:
9
Ответ: 45
Объяснение:
∠BMN = ∠BAC как накрест лежащие при пересечении параллельных прямых MN и АС секущей АВ,
∠В - общий для треугольников АВС и MBN, значит
ΔАВС подобен ΔMBN по двум углам.
Коэффициент подобия:
k = AC / MN = 16 / 12 = 4/3
Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
Sabc / Smbn = k²
Smbn = Sabc / k²
Smbn = 80 / (16/9) = 80 · 9/16 = 45 кв. ед.
Похожие вопросы
Предмет: Химия,
автор: valeevadarina08
Предмет: Математика,
автор: ilaisrailov66
Предмет: Английский язык,
автор: kirilldragunov99
Предмет: Алгебра,
автор: Kатюша69