Предмет: Алгебра,
автор: samurai1161
Двойной интеграл.Помогите пожалуйста.
Приложения:
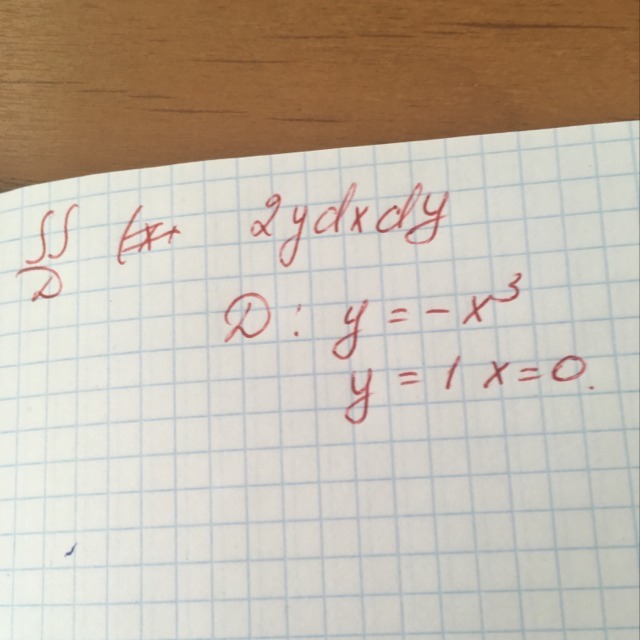
samurai1161:
Да
Ответы
Автор ответа:
1
Приложения:
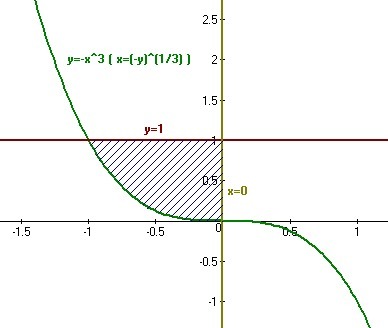
Похожие вопросы
Предмет: Химия,
автор: sevilibragimova59
Предмет: Қазақ тiлi,
автор: abdurahmanbaky82
Предмет: Русский язык,
автор: sanzharnauryzov
Предмет: Математика,
автор: nik11221
Предмет: Геометрия,
автор: Stalia1