Question

HELLLLP!!!! ПОМОГИИИИИТЕЕЕЕ ооооочень надороооо! Даю 100 баллов

Answer 1

Еще не поздно? Только все надо будет буквенными обозначениями переписать, конечно.

Answer 2

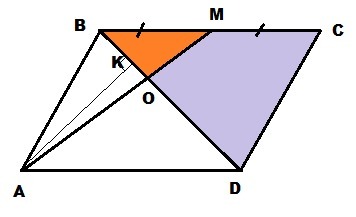
BC║AD  ⇒
∠MBO = ∠ADO;  ∠BMO = ∠DAO  - накрест лежащие углы  ⇒
ΔBOM ~ ΔDOA  по двум равным углам
BM = 1/2 BC = 1/2 AD  ⇒
$\frac{BO}{OD} =\frac{BM}{AD} = \frac{1}{2}$      
OD = 2 BO
Диагональ BD делит параллелограмм на два равных треугольника  ⇒
$S_{BCD}=S_{ABD}= \frac{1}{2} S_{ABCD}= \frac{1}{2} *30=15$ см²

$S_{ABC}=\frac{BD*AK}{2} = \frac{(BO+OD)*AK}{2} = \\ \\ =\frac{(BO+2BO)*AK}{2} =3*( \frac{BO*AK}{2} )=3S_{ABO} \\ 15 = 3S_{ABO} \\ S_{ABO}=5$
$S_{DOA}=S_{ABD}-S_{ABO}=15-5=10$ см²

ΔDOA ~ ΔBOM с коэффициентом подобия k=2  ⇒
Площади подобных треугольников относятся как коэффициент подобия в квадрате :
$\frac{S_{DOA}}{S_{BOM}} =k^2=4$
$S_{BOM}= \frac{1}{4} S_{DOA}= \frac{1}{4} *10=2,5$ см²
$S_{MODC}=S_{BCD}-S_{BOM}=15-2,5=12,5$ см²

Ответ: $S_{BOM}$ = 2,5 см²; $S_{MODC}$ =12,5 см²