Предмет: Математика,
автор: vikras97
Вычислить неопределенные интегралы
Приложения:
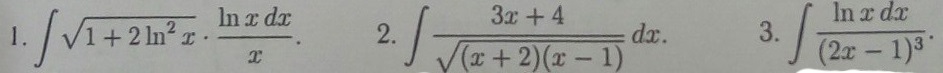
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Обществознание,
автор: homer271
Предмет: История,
автор: kotjavolkov
Предмет: Алгебра,
автор: borukgrru
Предмет: Математика,
автор: romellar
Предмет: Математика,
автор: gamerciklop