Предмет: Математика,
автор: andrei15181
найти производные функций, высшая математика
Приложения:
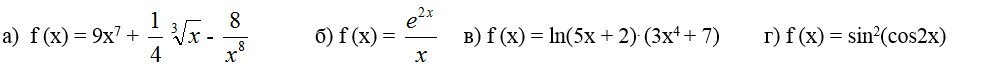
Ответы
Автор ответа:
2
а)
![f(x)= 9x^7+ \frac{1}{4} \sqrt[3]{x} - \frac{8}{x^8}=9x^7+ \frac{1}{4} x^{ \frac{1}{3} } - 8x^{-8} \\ \\ f'(x)= 9*7x^6+ \frac{1}{4} * \frac{1}{3} x^{- \frac{2}{3}} - 8*(-8)x^{-9}= \\ \\ =63x^6 + \frac{1}{12 \sqrt[3]{x^2} } + \frac{64}{x^9} f(x)= 9x^7+ \frac{1}{4} \sqrt[3]{x} - \frac{8}{x^8}=9x^7+ \frac{1}{4} x^{ \frac{1}{3} } - 8x^{-8} \\ \\ f'(x)= 9*7x^6+ \frac{1}{4} * \frac{1}{3} x^{- \frac{2}{3}} - 8*(-8)x^{-9}= \\ \\ =63x^6 + \frac{1}{12 \sqrt[3]{x^2} } + \frac{64}{x^9}](https://tex.z-dn.net/?f=f%28x%29%3D+9x%5E7%2B+%5Cfrac%7B1%7D%7B4%7D++%5Csqrt%5B3%5D%7Bx%7D+-+%5Cfrac%7B8%7D%7Bx%5E8%7D%3D9x%5E7%2B+%5Cfrac%7B1%7D%7B4%7D+x%5E%7B+%5Cfrac%7B1%7D%7B3%7D+%7D+-+8x%5E%7B-8%7D+++%5C%5C++%5C%5C+f%27%28x%29%3D+9%2A7x%5E6%2B+%5Cfrac%7B1%7D%7B4%7D+%2A+%5Cfrac%7B1%7D%7B3%7D++x%5E%7B-+%5Cfrac%7B2%7D%7B3%7D%7D++-+8%2A%28-8%29x%5E%7B-9%7D%3D+%5C%5C++%5C%5C+%3D63x%5E6+%2B+%5Cfrac%7B1%7D%7B12+%5Csqrt%5B3%5D%7Bx%5E2%7D+%7D+%2B+%5Cfrac%7B64%7D%7Bx%5E9%7D+)
б)

в)

г)
f(x) = sin²(cos2x)
f'(x) = 2sin(cos2x)*(cos2x)' = 2sin(cos2x)*(-sin2x*(2x)') =
= -4sin (cos2x)*sin2x
б)
в)
г)
f(x) = sin²(cos2x)
f'(x) = 2sin(cos2x)*(cos2x)' = 2sin(cos2x)*(-sin2x*(2x)') =
= -4sin (cos2x)*sin2x
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Геометрия,
автор: fokib54
Предмет: Українська література,
автор: D1panda
Предмет: История,
автор: ДанаДана12345
Предмет: Алгебра,
автор: АнастасияКвит