Предмет: Математика,
автор: ЛистЗолота
помогите решить систему уравнений
Приложения:
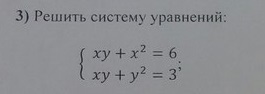
Ответы
Автор ответа:
5
cложим
xy+x^2+xy+y^2=3+6
x^2+2xy+y^2=9
(x+y)^2=9
получаем
1, x+y=3
2, x+y=-3
вычитаем
xy+x^2-xy-y^2=6-3
x^2-y^2=3
(x-y)(x+y)=3
подставляем
1. x+y=3
3(x-y)=3
x-y=1
2x=4
x=2
y=1
2. x+y=-3
-3(x-y)=3
x-y=-1
2x=-4
x=-2
y=-1
Ответ (-2 -1) (2 1)
xy+x^2+xy+y^2=3+6
x^2+2xy+y^2=9
(x+y)^2=9
получаем
1, x+y=3
2, x+y=-3
вычитаем
xy+x^2-xy-y^2=6-3
x^2-y^2=3
(x-y)(x+y)=3
подставляем
1. x+y=3
3(x-y)=3
x-y=1
2x=4
x=2
y=1
2. x+y=-3
-3(x-y)=3
x-y=-1
2x=-4
x=-2
y=-1
Ответ (-2 -1) (2 1)
Аноним:
верно
у меня правильно?
Автор ответа:
3
Дано:
{ xy + x^2 = 6
{ xy + y^2 = 3
Решение:
{ x(y + x) = 6
{ y(x + y) = 3
x/y = 2
x = 2y
2y • y + y^2 = 3
{ y = 1
{ y = – 1
{ x • 1 + x^2 = 6
{ x • (– 1) + x^2 = 6
{ x = 2
{ x = – 3
{ x = 3
{ x = – 2
(x1 ; y1) = (2 ; 1)
(x2 ; y2) = (– 3 ; 1)
(x3 ; y3) = (3 ; – 1)
(x4 ; y4) = (– 2 ; – 1)
{ 2 • 1 + 2^2 = 6
{ 2 • 1 + 1^2 = 3
{ – 3 • 1 + (– 3)^2 = 6
{ – 3 • 1 + 1^2 = 3
{ 3 • (– 1) + 3^2 = 6
{ 3 • (– 1) + (– 1)^2 = 3
{ – 2 • (– 1) + (– 2)^2 = 6
{ – 2 • (– 1) + (– 1)^2 = 3
{ 6 = 6
{ 3 = 3
{ 6 = 6
{ – 2 = 3
{ 6 = 6
{ – 2 = 3
{ 6 = 6
{ 3 = 3
(x1 ; y1) = (2 ; 1)
(x2 ; y2) = (– 2 ; 1)
{ xy + x^2 = 6
{ xy + y^2 = 3
Решение:
{ x(y + x) = 6
{ y(x + y) = 3
x/y = 2
x = 2y
2y • y + y^2 = 3
{ y = 1
{ y = – 1
{ x • 1 + x^2 = 6
{ x • (– 1) + x^2 = 6
{ x = 2
{ x = – 3
{ x = 3
{ x = – 2
(x1 ; y1) = (2 ; 1)
(x2 ; y2) = (– 3 ; 1)
(x3 ; y3) = (3 ; – 1)
(x4 ; y4) = (– 2 ; – 1)
{ 2 • 1 + 2^2 = 6
{ 2 • 1 + 1^2 = 3
{ – 3 • 1 + (– 3)^2 = 6
{ – 3 • 1 + 1^2 = 3
{ 3 • (– 1) + 3^2 = 6
{ 3 • (– 1) + (– 1)^2 = 3
{ – 2 • (– 1) + (– 2)^2 = 6
{ – 2 • (– 1) + (– 1)^2 = 3
{ 6 = 6
{ 3 = 3
{ 6 = 6
{ – 2 = 3
{ 6 = 6
{ – 2 = 3
{ 6 = 6
{ 3 = 3
(x1 ; y1) = (2 ; 1)
(x2 ; y2) = (– 2 ; 1)
нельзя делить , когда не знаешь чисел. можно поделить на 0, необходимо это проверять
Похожие вопросы
Предмет: Физика,
автор: DikayaRoza
Предмет: Химия,
автор: ifasjon
Предмет: Геометрия,
автор: nikitaartemenko02
Предмет: Математика,
автор: дьего