Предмет: Математика,
автор: dalpaeva
Помогите ,пожалуйста,вычислить предел функции
Приложения:
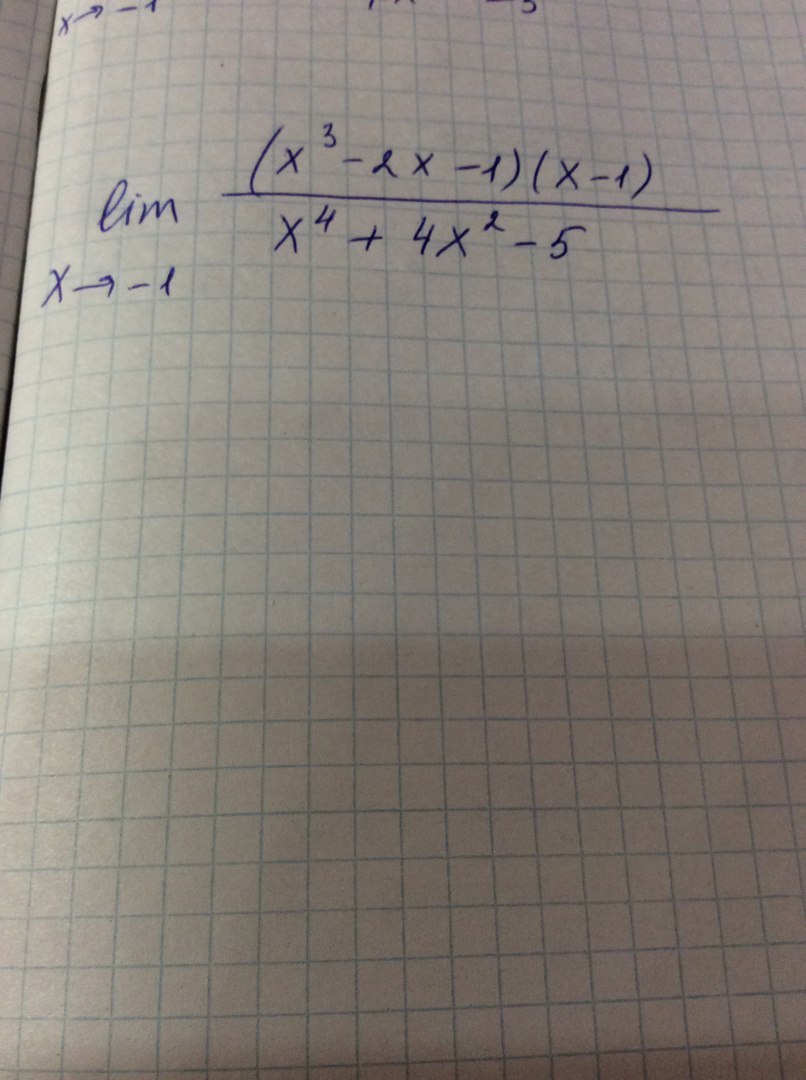
Ответы
Автор ответа:
1
Как итог, предел равен 1 при х, стремящимся к бесконечности
dalpaeva:
спасибо большое за решение,а не могли бы вы подробнее расписать,как скобки эти раскрывали ,как получился такой числитель и знаменатель
Вот это посложнее будет...
Ну, кубическое я раскладывал так: сразу видно по коэффициентам, что -1 является корнем этого уравнения. Тогда я это самое уравнение поделил уголком на x-(-1)=x+1 и получил x^2-x-1.
В знаменателе x^2 можно взять за отдельную переменную, тогда получается квадратное уравнение относительно x^2.
P.S. В последнем пункте, если я правильно помню, это называется биквадратным уравнением
Ну, кубическое я раскладывал так: сразу видно по коэффициентам, что -1 является корнем этого уравнения. Тогда я это самое уравнение поделил уголком на x-(-1)=x+1 и получил x^2-x-1.
В знаменателе x^2 можно взять за отдельную переменную, тогда получается квадратное уравнение относительно x^2.
P.S. В последнем пункте, если я правильно помню, это называется биквадратным уравнением
спасиюо)
спасибо)
Всегда пожалуйста!
Похожие вопросы
Предмет: Английский язык,
автор: Neroyfraighdj
Предмет: Алгебра,
автор: kruglovaa
Предмет: Физика,
автор: kravcenkokosta94
Предмет: Алгебра,
автор: ученик834
Предмет: Геометрия,
автор: oleggrah