Предмет: Алгебра,
автор: dasew123321
Помогите очень надо!!!!!!
Приложения:

Ответы
Автор ответа:
1
..........................
Приложения:
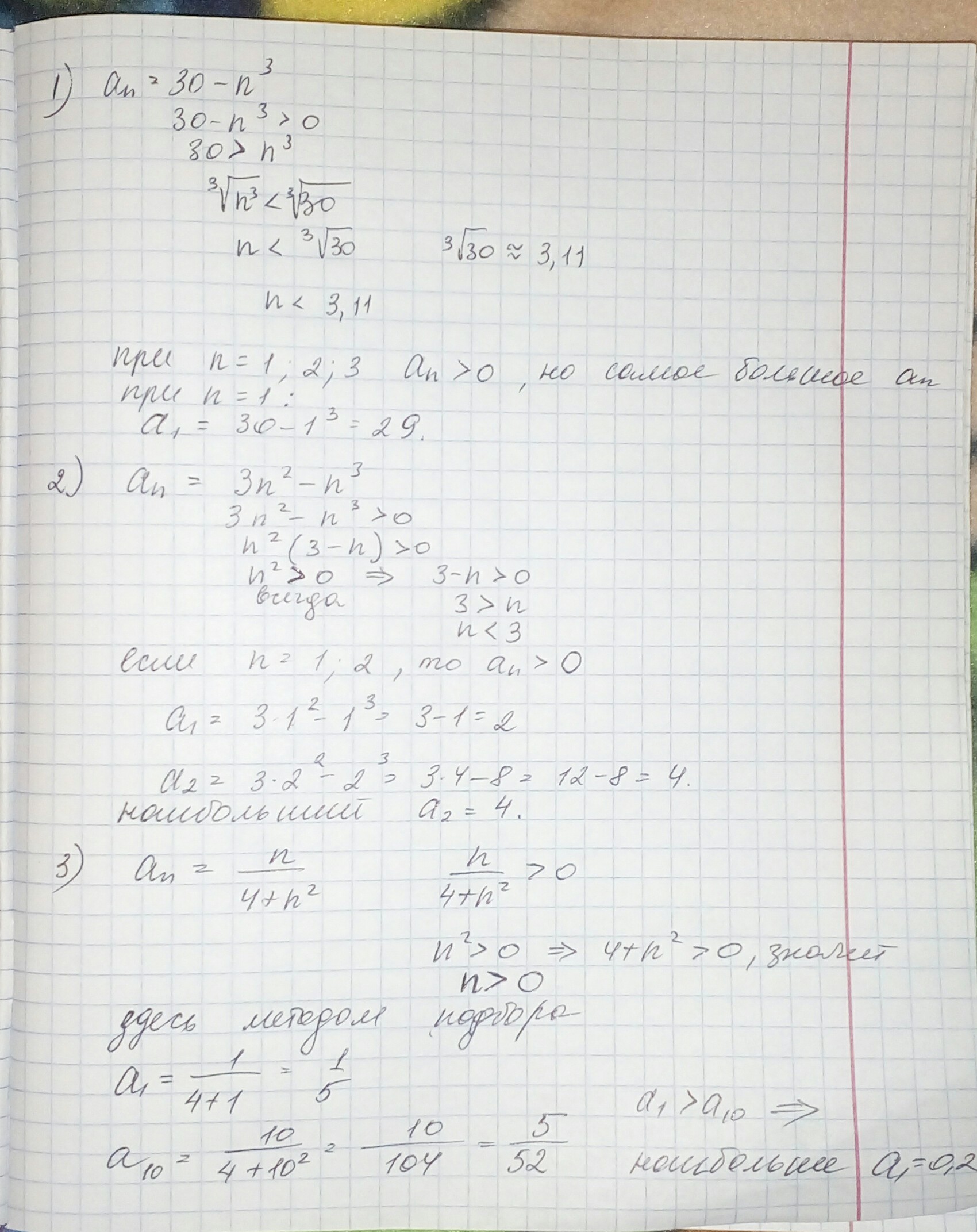
dasew123321:
cgc
Автор ответа:
1
1. Нам нужно, чтобы 30-n^3 ----> max
Для этого надо, чтобы n^3 ----> min
Самое маленькое натуральное число - 1 => a1=30-1^3=29 - наибольший член последовательности
2. 3n^2-n^3=n^2(3-n) ----> max
Нам нужно, чтобы 3-n>0, 0<n<3
То есть либо n=1, либо n=2
При n=1 1^2(3-1)=2
При n=2 2^2(3-2)=4 - наибольший член последовательности
3. an=n/(4+n^2)
Знаменатель всегда положителен, то есть, чтобы дробь была наибольшей, нужно чтобы n ----> min, посмотрим n от 1 до 5
a1=1/5
a2=1/4
a3=3/13
a4=1/5
a5=5/29
Следовательно, a2 = 1/4 - наибольший член последовательности
Для этого надо, чтобы n^3 ----> min
Самое маленькое натуральное число - 1 => a1=30-1^3=29 - наибольший член последовательности
2. 3n^2-n^3=n^2(3-n) ----> max
Нам нужно, чтобы 3-n>0, 0<n<3
То есть либо n=1, либо n=2
При n=1 1^2(3-1)=2
При n=2 2^2(3-2)=4 - наибольший член последовательности
3. an=n/(4+n^2)
Знаменатель всегда положителен, то есть, чтобы дробь была наибольшей, нужно чтобы n ----> min, посмотрим n от 1 до 5
a1=1/5
a2=1/4
a3=3/13
a4=1/5
a5=5/29
Следовательно, a2 = 1/4 - наибольший член последовательности
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: kapralovalejla04
Предмет: Биология,
автор: troshindima888
Предмет: Математика,
автор: Milutka
Предмет: Биология,
автор: Snowflake2000