Предмет: Математика,
автор: Аноним
Помогите нужно решить срочно
Приложения:
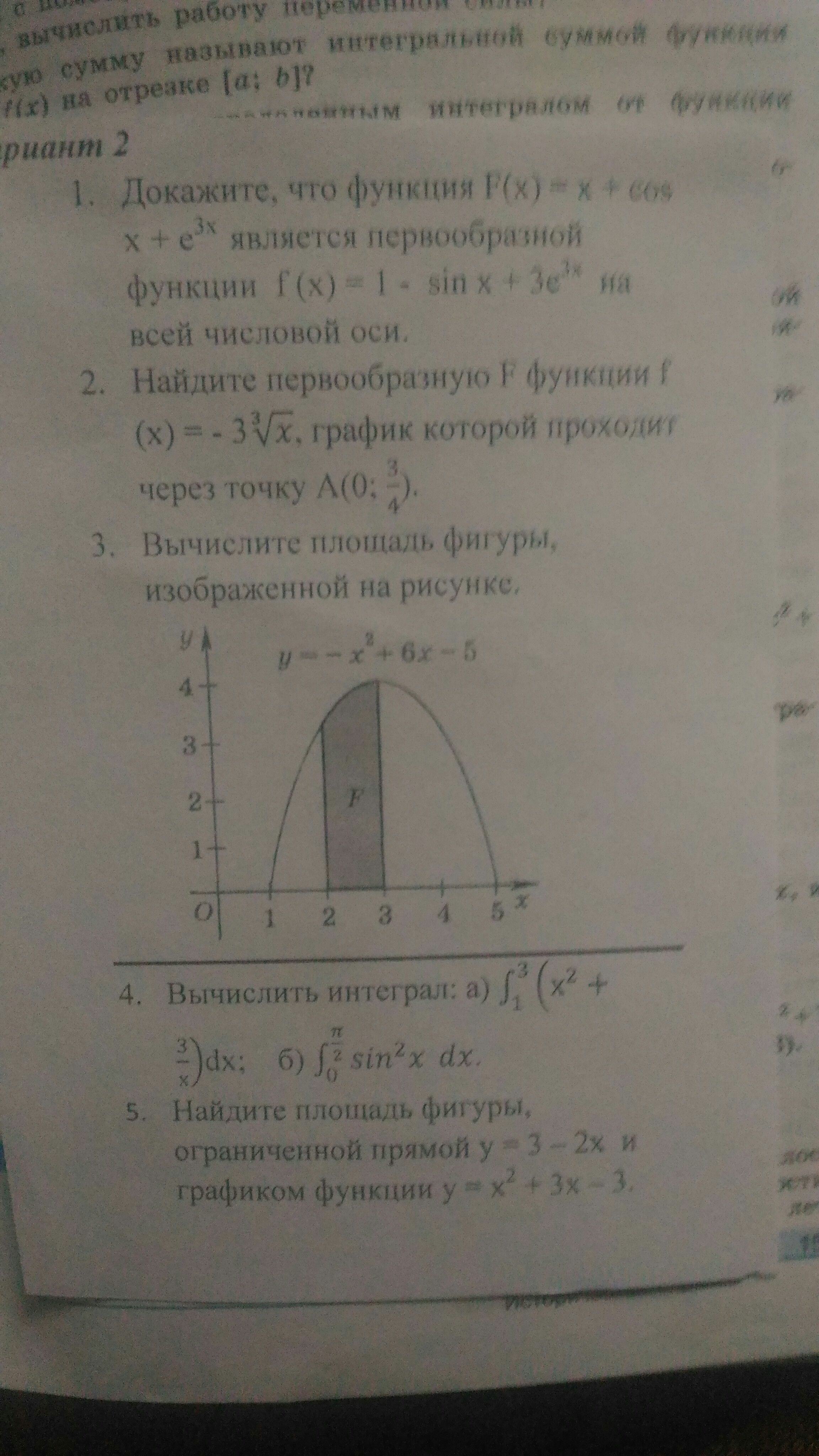
Ответы
Автор ответа:
1
1)  чтд
чтд
2)![f(x) = -3 \sqrt[3]{x} \\
F(x) = \int\limits { -3 \sqrt[3]{x}} \, dx = \int\limits {-3 x^{\frac{1}{3}} } \, dx = \frac{-3}{ \frac{1}{3}+1} x^{\frac{1}{3}+1} = \frac{-9}{4} x^{\frac{4}{3}} + C \\
\frac{3}{4} = 0 \cdot \frac{-9}{4}+C \\
C=\frac{3}{4} \\
F(x) = -\frac{9}{4} x^{\frac{4}{3}} + \frac{3}{4} f(x) = -3 \sqrt[3]{x} \\
F(x) = \int\limits { -3 \sqrt[3]{x}} \, dx = \int\limits {-3 x^{\frac{1}{3}} } \, dx = \frac{-3}{ \frac{1}{3}+1} x^{\frac{1}{3}+1} = \frac{-9}{4} x^{\frac{4}{3}} + C \\
\frac{3}{4} = 0 \cdot \frac{-9}{4}+C \\
C=\frac{3}{4} \\
F(x) = -\frac{9}{4} x^{\frac{4}{3}} + \frac{3}{4}](https://tex.z-dn.net/?f=++f%28x%29+%3D+-3+%5Csqrt%5B3%5D%7Bx%7D+%5C%5C%0A+F%28x%29+%3D++%5Cint%5Climits+%7B+-3+%5Csqrt%5B3%5D%7Bx%7D%7D+%5C%2C+dx+%3D++%5Cint%5Climits+++++%7B-3+x%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D+%7D+%5C%2C+dx+%3D++%5Cfrac%7B-3%7D%7B+%5Cfrac%7B1%7D%7B3%7D%2B1%7D+x%5E%7B%5Cfrac%7B1%7D%7B3%7D%2B1%7D+%3D++%5Cfrac%7B-9%7D%7B4%7D+x%5E%7B%5Cfrac%7B4%7D%7B3%7D%7D+%2B+C+%5C%5C+%0A+++%5Cfrac%7B3%7D%7B4%7D+%3D++0+%5Ccdot+%5Cfrac%7B-9%7D%7B4%7D%2BC+%5C%5C+%0A+C%3D%5Cfrac%7B3%7D%7B4%7D+%5C%5C%0A+F%28x%29+%3D+-%5Cfrac%7B9%7D%7B4%7D+x%5E%7B%5Cfrac%7B4%7D%7B3%7D%7D+%2B+%5Cfrac%7B3%7D%7B4%7D+)
3)
4)
5)

2)
3)
4)
5)
Похожие вопросы
Предмет: Физика,
автор: nastyssst
Предмет: Математика,
автор: knazukkirill9
Предмет: Математика,
автор: margomirzak
Предмет: Алгебра,
автор: superjcen
Предмет: Литература,
автор: Новичок111112002
2) [tex]- \frac{9}{4}x^{ \frac{4}{3}} + \frac{3}{4}[/tex]