Предмет: Алгебра,
автор: kiralaitrichter
Найдите значение выражения: lg 1\5+ log100 25.
Найдите значение выражения: lоg100 4 + lg 1\2
Приложения:
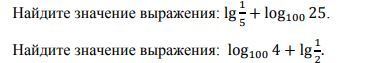
Ответы
Автор ответа:
3
Похожие вопросы
Предмет: Алгебра,
автор: yduduc
Предмет: Математика,
автор: anderyvolkov09
Предмет: Английский язык,
автор: zkhzkhzkh
Предмет: Алгебра,
автор: izabellafortuna
Предмет: Литература,
автор: alenka2005ГОД