Предмет: Алгебра,
автор: German22848
Решите пожалуйста неравенство БЕЗ метода рационализации
Приложения:
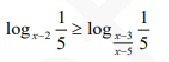
Ответы
Автор ответа:
2
ОДЗ:
{x-2>0
{x-2≠1
{(x-3)/(x-5)>0
{(x-3)/(x-5)≠1
{x≠5
x∈(2;3)U(5;+∞)
перейдем к основанию 5
знак сохраняем
D=64-4*13=64-52=12=4*3
x₁=4+√3
x₂=4-√3
решаем методом интервалов
-------[4-√3]++++++(5)---------[4+√3]+++++++
x∈[4-√3;5)U[4+√3;+∞)
с учетом ОДЗ, получаем ответ
x∈[4-√3;3)U[4+√3;+∞)
Похожие вопросы
Предмет: Информатика,
автор: neowilo21
Предмет: Геометрия,
автор: trapg
Предмет: Химия,
автор: hyewoniz
Предмет: Физика,
автор: ЕАР2002
Предмет: Математика,
автор: antojka