Предмет: Алгебра,
автор: viktorsokolov1
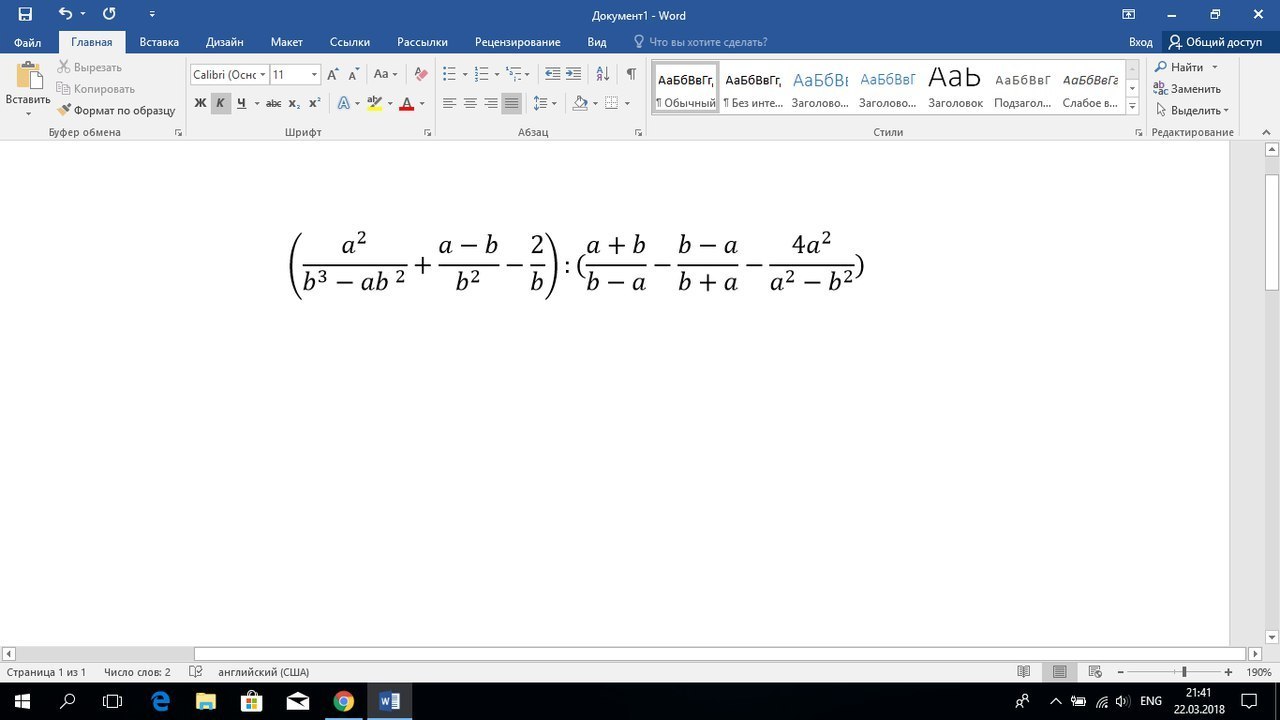
даю 34 балла, пожалуйста быстрее, решите уравнение
Приложения:
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: serebryanskaya2447
Предмет: Математика,
автор: alenik62
Предмет: История,
автор: artemovaelena1107
Предмет: Биология,
автор: асема2005