Предмет: Геометрия,
автор: maksim403
В треугольнике ABC известны стороны: AB=15, BC=25 и AC=16. Прямая проходящая через вершину A перпендикулярно биссектрисе треугольника BN, пересекает сторону BC в точке M. Докажите, что биссектриса угла C делит пополам отрезок MN
maksim403:
Помогите пожалуйста,Срочно надо.
Ответы
Автор ответа:
33
Треугольник АВМ по построению - равнобедренный, АВ = ВМ = 15.
Отрезок МС = 25 - 15 = 10.
Сторона АС делится точкой N в отношении 15/25 = 3/5.
Отрезок NС = 16*5/8 = 10.
То есть треугольник CMN - равнобедренный.
Поэтому биссектриса угла С делит основание его MN пополам.
Отрезок МС = 25 - 15 = 10.
Сторона АС делится точкой N в отношении 15/25 = 3/5.
Отрезок NС = 16*5/8 = 10.
То есть треугольник CMN - равнобедренный.
Поэтому биссектриса угла С делит основание его MN пополам.
Приложения:
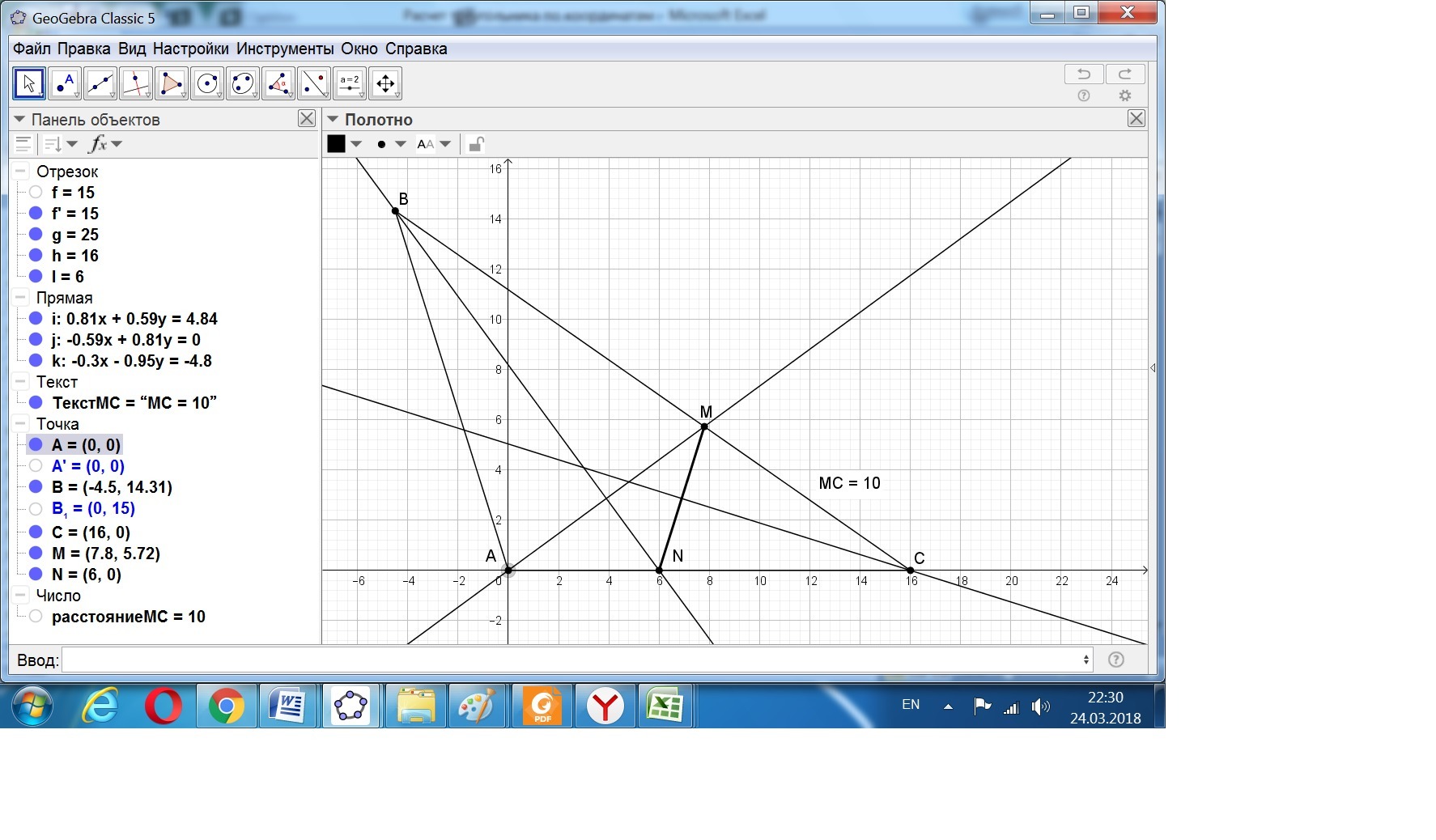
откуда 5\8???
Похожие вопросы
Предмет: Литература,
автор: tatanaivanilova08
Предмет: Алгебра,
автор: anatoliy2004yakovysh
Предмет: Геометрия,
автор: rejmgenn
Предмет: География,
автор: dfhdfjyscvjdfj
Предмет: Обществознание,
автор: ahatalieva