Предмет: Математика,
автор: Ghost000
дифференциальные уравнения второго порядка, поподробнее будьте добры
Приложения:
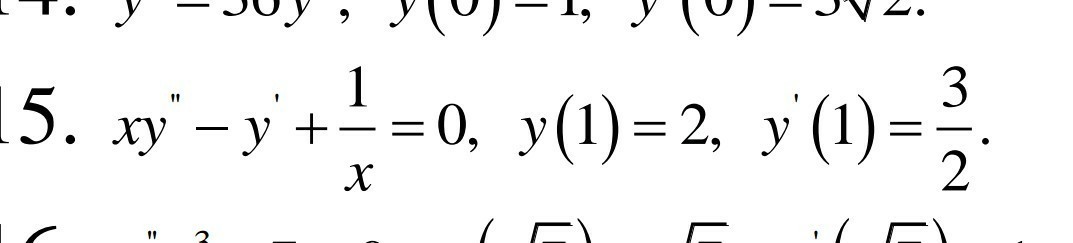
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: bkv321089
Предмет: Русский язык,
автор: ilgam07
Предмет: Английский язык,
автор: vovkamarkovka2019
Предмет: Математика,
автор: BetMan717