Предмет: Алгебра,
автор: zvarichr
Решите пожалуйста 4,5,6,7 номера
( желательно на листочке)
Приложения:
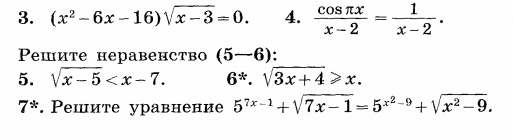
Ответы
Автор ответа:
1
4. 
5.
6.![\sqrt{3x+4} \geq x\\
(x \geq 0\ \ and\ \ 3x+4 \geq x^2)\ \ or\ \ (x\ \textless \ 0\ \ and\ \ 3x+4 \geq 0)\\
(x \geq 0\ \ and\ \ x^2-3x-4 \leq 0)\ \ or\ \ (x\ \textless \ 0\ \ and\ \ x \geq -\frac{4}{3})\\
(x \geq 0\ \ and\ \ (x+1)(x-4) \leq 0)\ \ or\ \ x\in[-\frac{4}{3};0)\\
(x\in[0;+\infty)\ \ and\ \ x\in[-1;4])\ \ or\ \ x\in[-\frac{4}{3};0)\\
x\in[0;4]\ \ or\ \ x\in[-\frac{4}{3};0)\\
x\in[-\frac{4}{3};4] \sqrt{3x+4} \geq x\\
(x \geq 0\ \ and\ \ 3x+4 \geq x^2)\ \ or\ \ (x\ \textless \ 0\ \ and\ \ 3x+4 \geq 0)\\
(x \geq 0\ \ and\ \ x^2-3x-4 \leq 0)\ \ or\ \ (x\ \textless \ 0\ \ and\ \ x \geq -\frac{4}{3})\\
(x \geq 0\ \ and\ \ (x+1)(x-4) \leq 0)\ \ or\ \ x\in[-\frac{4}{3};0)\\
(x\in[0;+\infty)\ \ and\ \ x\in[-1;4])\ \ or\ \ x\in[-\frac{4}{3};0)\\
x\in[0;4]\ \ or\ \ x\in[-\frac{4}{3};0)\\
x\in[-\frac{4}{3};4]](https://tex.z-dn.net/?f=+%5Csqrt%7B3x%2B4%7D+%5Cgeq+x%5C%5C%0A%28x+%5Cgeq+0%5C+%5C+and%5C+%5C+3x%2B4+%5Cgeq+x%5E2%29%5C+%5C+or%5C+%5C+%28x%5C+%5Ctextless+%5C+0%5C+%5C+and%5C+%5C+3x%2B4+%5Cgeq+0%29%5C%5C%0A%28x+%5Cgeq+0%5C+%5C+and%5C+%5C+x%5E2-3x-4+%5Cleq+0%29%5C+%5C+or%5C+%5C+%28x%5C+%5Ctextless+%5C+0%5C+%5C+and%5C+%5C+x+%5Cgeq+-%5Cfrac%7B4%7D%7B3%7D%29%5C%5C%0A%28x+%5Cgeq+0%5C+%5C+and%5C+%5C+%28x%2B1%29%28x-4%29+%5Cleq+0%29%5C+%5C+or%5C+%5C+x%5Cin%5B-%5Cfrac%7B4%7D%7B3%7D%3B0%29%5C%5C%0A%28x%5Cin%5B0%3B%2B%5Cinfty%29%5C+%5C+and%5C+%5C+x%5Cin%5B-1%3B4%5D%29%5C+%5C+or%5C+%5C+x%5Cin%5B-%5Cfrac%7B4%7D%7B3%7D%3B0%29%5C%5C%0Ax%5Cin%5B0%3B4%5D%5C+%5C+or%5C+%5C+x%5Cin%5B-%5Cfrac%7B4%7D%7B3%7D%3B0%29%5C%5C%0Ax%5Cin%5B-%5Cfrac%7B4%7D%7B3%7D%3B4%5D)
7.
Нас интересует указанное уравнение на следующем промежутке значений для агрумента :
:
![7x-1 \geq 0\ \ and\ \ x^2-9 \geq 0\\
x\in[\frac{1}{7};+\infty)\ \ and\ \ x\in(-\infty;-3]\cup[3;+\infty)\\
x\in[3;+\infty) 7x-1 \geq 0\ \ and\ \ x^2-9 \geq 0\\
x\in[\frac{1}{7};+\infty)\ \ and\ \ x\in(-\infty;-3]\cup[3;+\infty)\\
x\in[3;+\infty)](https://tex.z-dn.net/?f=7x-1+%5Cgeq+0%5C+%5C+and%5C+%5C+x%5E2-9+%5Cgeq+0%5C%5C%0Ax%5Cin%5B%5Cfrac%7B1%7D%7B7%7D%3B%2B%5Cinfty%29%5C+%5C+and%5C+%5C+x%5Cin%28-%5Cinfty%3B-3%5D%5Ccup%5B3%3B%2B%5Cinfty%29%5C%5C%0Ax%5Cin%5B3%3B%2B%5Cinfty%29)
на указанном промежутке как выражение так и выражение
так и выражение  являються суммами двух МОННОТОННО РАСТУЩИХ функций
являються суммами двух МОННОТОННО РАСТУЩИХ функций
при чем свой рост первая сумма начинает с значения
а вторая с значения
и тут важно увидеть, что темп роста (скорость роста) первой суммы, как функции, ниже темпа роста второй суммы, как функции, так как в первой сумме фигурирует выражение , а во второй
, а во второй  (на интересующем нас интервале значений икс)
(на интересующем нас интервале значений икс)
и также критически важно заметить, что скорость роста темпа (скорости) роста второй функции с ростом аргумента, только растет, также как и в случае с первой, это можно показать через первую и вторую производные на интересующем нас промежутке
Все это означает, что в какой-то момент вторая сумма, как функция, "догонит" первую сумму, которая рассматриваеться как функция, и после этого момента вторая сумма будет иметь гарантированно большие значения, чем первая, а это означает, что уравнение имеет только одно решение.
"Угадаем его"!


Ответ:
5.
6.
7.
Нас интересует указанное уравнение на следующем промежутке значений для агрумента
на указанном промежутке как выражение
при чем свой рост первая сумма начинает с значения
а вторая с значения
и тут важно увидеть, что темп роста (скорость роста) первой суммы, как функции, ниже темпа роста второй суммы, как функции, так как в первой сумме фигурирует выражение
и также критически важно заметить, что скорость роста темпа (скорости) роста второй функции с ростом аргумента, только растет, также как и в случае с первой, это можно показать через первую и вторую производные на интересующем нас промежутке
Все это означает, что в какой-то момент вторая сумма, как функция, "догонит" первую сумму, которая рассматриваеться как функция, и после этого момента вторая сумма будет иметь гарантированно большие значения, чем первая, а это означает, что уравнение имеет только одно решение.
"Угадаем его"!
Ответ:
Похожие вопросы
Предмет: История,
автор: litvinkonastasya
Предмет: История,
автор: ronypony2022
Предмет: Право,
автор: vanyahandysenko
Предмет: Математика,
автор: красав4ик003