Question

В наклонной призме abcda1b1c1d1 основанием является параллелограмм ab=3
ad=7 bd=6 aa1=10 найти площадь призмы

Answer 1

Sбок =P⊥ *DD1 =6(2+√3)
(P⊥ - периметр перпендикулярного сечения)

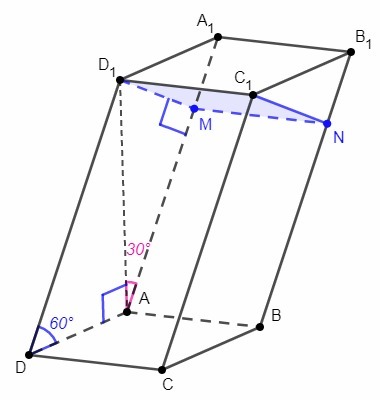
D1C1NM - перпендикулярное сечение, D1M⊥AA1,
D1C1NM - параллелограмм.

P(D1C1NM) =2(D1C1 +D1M)

D1A⊥ABC, A - проекция D1 на ABC, DA - проекция DD1 на ABC.
∠D1DA=60°, ∠D1AA1=30°

D1C1 =DA (ABCD и A1B1C1D1 - основания призмы, равные квадраты)

D1C1 =DA =D1A/√3
D1M =D1A/2
DD1 =2D1A/√3

Sбок =2DD1*(D1C1 +D1M) =
4D1A/√3 *(D1A/√3 +D1A/2) =
D1A^2 *2(2+√3)/3

D1A^2 *2(2+√3)/3 =6(2+√3) <=> D1A=3