Предмет: Алгебра,
автор: Kishikova2016
Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 34 больше произведения двух других чисел.
Ответы
Автор ответа:
0
……);:....................
Приложения:
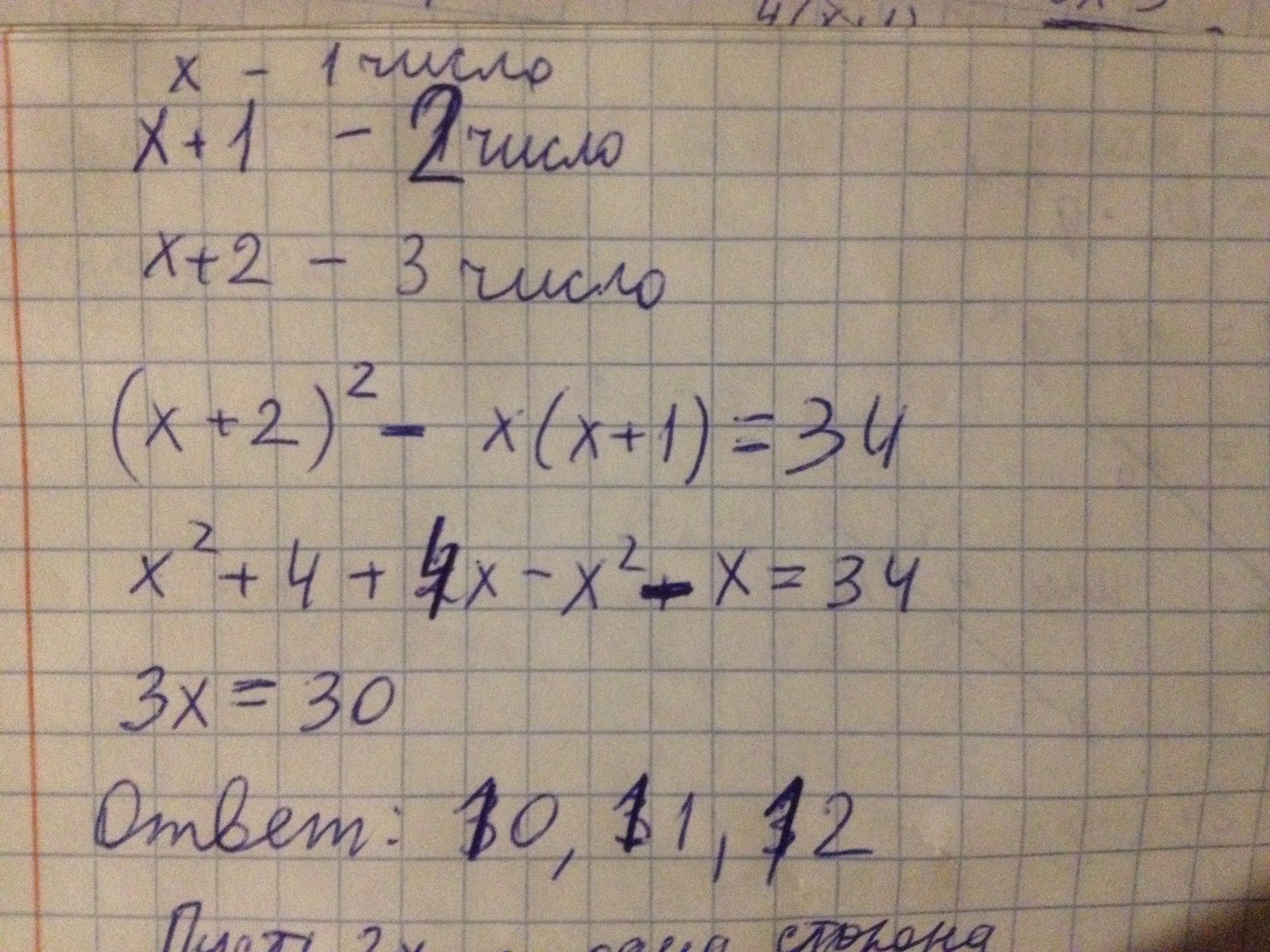
Автор ответа:
0
I число n
II число (n+1)
III число (n + 1 + 1) = (n+2)
Уравнение:
(n+2)² - n(n+1) = 34
n² + 2*n*2 + 2² - n*n - n*1 =34
n² + 4n + 4 - n² - n = 34
(n² - n²) + (4n - n) + 4 = 34
3n + 4 = 34
3n = 34 - 4
3n = 30
n = 30 : 3
n=10 - I число
10 + 1 = 11 - II число
10 + 2 = 12 - III число
Ответ : 10, 11 , 12 .
II число (n+1)
III число (n + 1 + 1) = (n+2)
Уравнение:
(n+2)² - n(n+1) = 34
n² + 2*n*2 + 2² - n*n - n*1 =34
n² + 4n + 4 - n² - n = 34
(n² - n²) + (4n - n) + 4 = 34
3n + 4 = 34
3n = 34 - 4
3n = 30
n = 30 : 3
n=10 - I число
10 + 1 = 11 - II число
10 + 2 = 12 - III число
Ответ : 10, 11 , 12 .
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Алгебра,
автор: ChuayNakahara60
Предмет: История,
автор: gritsuckalesha
Предмет: Биология,
автор: fatosh57
Предмет: Математика,
автор: ярик172