Question

Помогите пожалуйста. Не поняла как решить эту задачу.
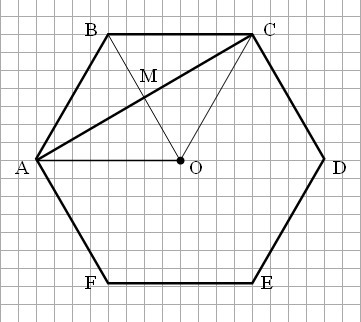
ABCDEF- правильный шестиугольник. Диагональ АС равна $8 \sqrt{3}$ . Найдите площадь шестиугольника. Желательно расписать с формулами и с пояснениями.

Answer 1

Рассмотрим ▲АВС. Это равнобедренный ▲, так как АВ=ВС ∠АВС=120°
На сторону АС из вершины В опустим высоту ВН. АН=НС=8√3/2=4√3
Рассмотрим ▲АВН, ∠АНВ=90°, ∠АВН=∠АВС/2=120/2=60°
∠ВАН=180-(90+60)=30°
Пусть ВН=х, тогда АВ=2*ВН=2*х, как катет прямоугольного треугольника, лежащий против угла 30°.
По теореме Пифагора АН=√(АВ²-ВН²)  4√3=√((2*х)²-х²)=√3*х²=х√3   х=4
АВ=2*х=2*4=8
S(ABCDEF)=a²*3√3/2=8²*3√3/2=96√3

Answer 2

Площадь правильного шестиугольника: S = 1/2 * 3a²√3
Так как ∠АВС = 120°, то ΔАВО - равносторонний и ∠АВО = 60°
АВСО - ромб  и  ВО⊥АС

Так как АС/2 = АМ = АВ*sin60°, то:
                                        а = АВ = АМ : sin60° = 4√3 : √3/2 = 8

Площадь шестиугольника:
             S = 1/2 * 3*64√3 = 96√3 ≈ 166,28 (ед.²)