Question

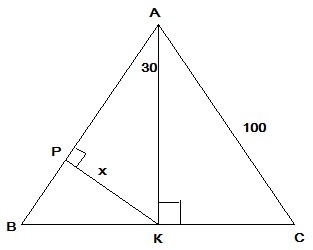
Тругольник ABC равносторонний. AK-биссектриса. Найти расстояние от точки K до стороны AC, если периметр треугольника равен 300 см.

Answer 1

В равностороннем треугольнике биссектриса является высотой и медианой, поэтому найдем высоту АК по теореме Пифагора:
АК²=АВ²-ВК², ВК=1/2ВС, ВС=300/3=100см, ВК=100/2см⇒
АК²=10000-10000/4=30000/4⇒ АК=√30000/4=50√3см.
В ΔАКР ∠ВАК=1/2∠А=60/2=30°⇒РК=1/2АК -катет прямоугольного треугольника, лежащий против угла 30° равен половине гипотенузы⇒
РК=1/2АК=50√3/2=25√3см.

Answer 2

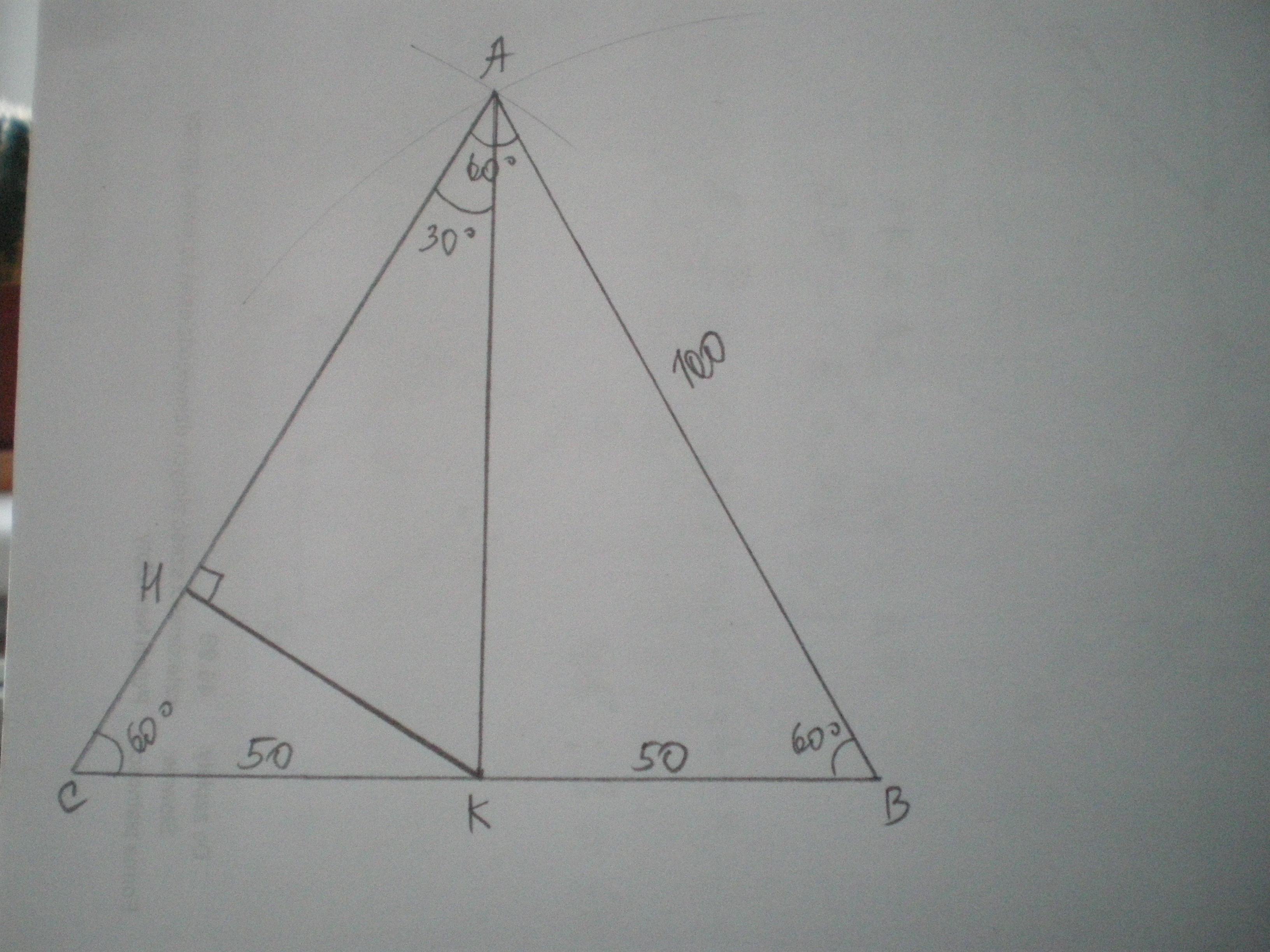
Дано: Δ АВС - равносторонний, Р=300 см. АК - биссектриса, высота.
Найти КН.

Найдем стороны треугольника АВС
АВ=ВС=АС=300:3=100 см

Найдем АК из Δ АВК по теореме Пифагора:
АК=√(АВ²-ВК²)=√(10000-2500)=√7500=86,6 см.

В равностороннем треугольнике все углы равны 60 градусов. 
Поэтому ∠КАН=60:2=30°  и КН=1\2 АК
КН=86,6:2=43,3 см.

Ответ: 43, 3 см.