Предмет: Математика,
автор: Shanon
интеграл неопределенный
Приложения:
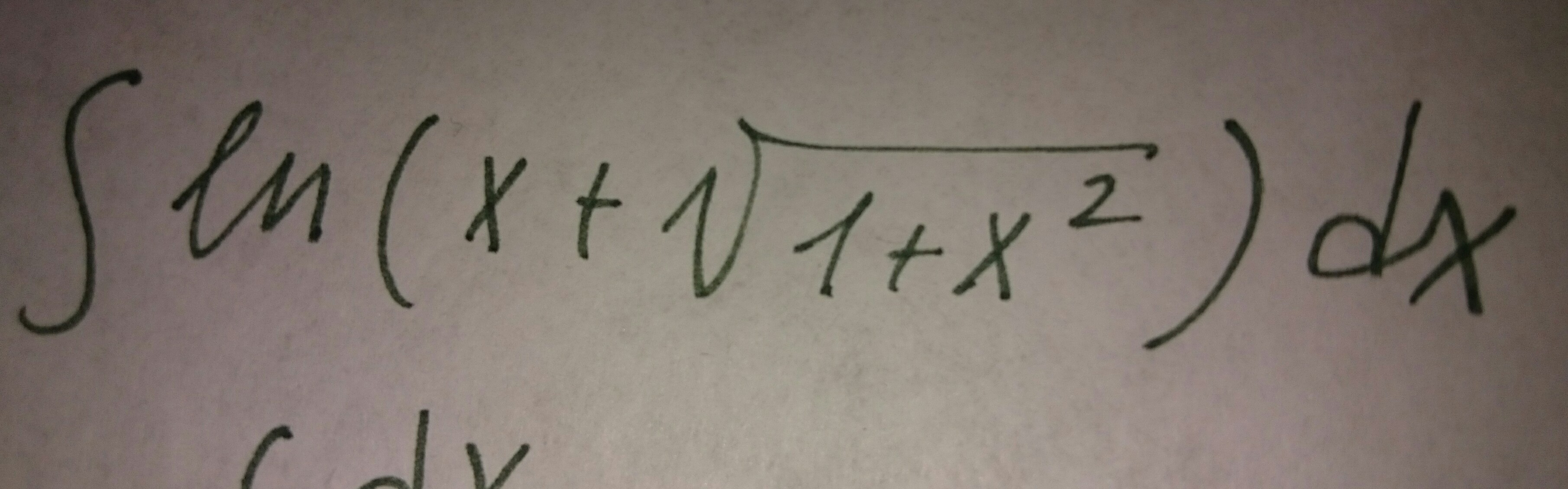
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: География,
автор: ovoalvlvragcovl
Предмет: Математика,
автор: 00Sata00
Предмет: Алгебра,
автор: oona21169
Предмет: Алгебра,
автор: mimoza17