Предмет: Алгебра,
автор: N0len
упростите выражение:
Приложения:
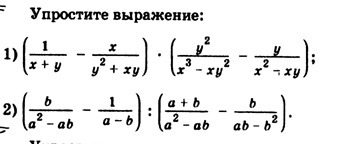
Ответы
Автор ответа:
0
1)

2)


2)
Похожие вопросы
Предмет: Русский язык,
автор: yorkshirbessi
Предмет: Литература,
автор: erttrrtt69
Предмет: История,
автор: alinanurlybau
Предмет: Алгебра,
автор: dianaislamova
Предмет: Алгебра,
автор: herobrine144