Предмет: Геометрия,
автор: anydasha
Найдите площадь треугольника, который образован в результате пересечения координатных осей и прямой 2y-4x-5=0
Ответы
Автор ответа:
1
Шаг 1.2y-4x-5=0 преобразуем уравнение прямой
-4х+2у=5 разделим всё на пять
-4х/5 +2у/5 =1 оставим икс и игрек в числителях
х/(-1целая1/4) +у/2,5=1 - это уравнение прямой в отрезках на
координатных осях.
Шаг 2.А теперь постройте данную прямую:
сначала оси Ох и Оу и числа положительные и отрицательные;
потом на оси Ох (горизонтальной) найдите -1целую1/4 и
обозначте точкой А;
потом на оси Оу (вертикальной) найдите 2,5 и
обозначте точкой В;
соедините прямой точки А и В, но постройте не отрезок АВ, а
прямую, то есть за пределы А и В должны выйти "хвостики".
Шаг 3.Дальше - Вы увидите на рисунке треугольник АОВ (т.О - начало координат, "перекрёсток" координатных прямых). Этот треугольник слегка заштрихуйте простым карандашом.
Шаг 4.S(площадь треугольника)=1/2 *АО*ВО=0,5 *1,25*2,5=1,5625≈1,6(кв.ед.)
Ответ: 1,5625 квадратных единиц.
-4х+2у=5 разделим всё на пять
-4х/5 +2у/5 =1 оставим икс и игрек в числителях
х/(-1целая1/4) +у/2,5=1 - это уравнение прямой в отрезках на
координатных осях.
Шаг 2.А теперь постройте данную прямую:
сначала оси Ох и Оу и числа положительные и отрицательные;
потом на оси Ох (горизонтальной) найдите -1целую1/4 и
обозначте точкой А;
потом на оси Оу (вертикальной) найдите 2,5 и
обозначте точкой В;
соедините прямой точки А и В, но постройте не отрезок АВ, а
прямую, то есть за пределы А и В должны выйти "хвостики".
Шаг 3.Дальше - Вы увидите на рисунке треугольник АОВ (т.О - начало координат, "перекрёсток" координатных прямых). Этот треугольник слегка заштрихуйте простым карандашом.
Шаг 4.S(площадь треугольника)=1/2 *АО*ВО=0,5 *1,25*2,5=1,5625≈1,6(кв.ед.)
Ответ: 1,5625 квадратных единиц.
Автор ответа:
1
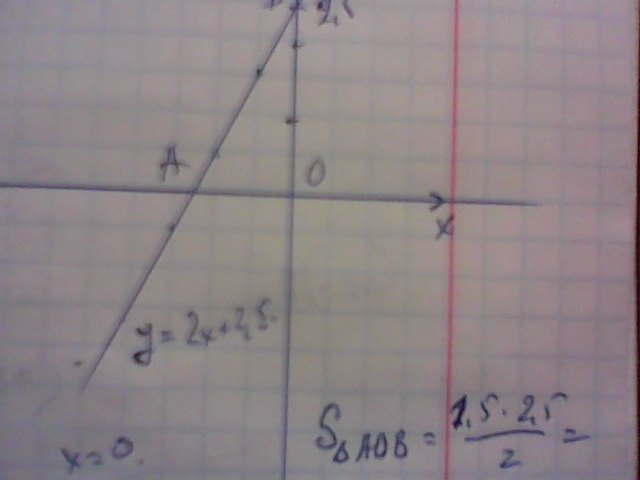
Смотри фото
2у-4х-5=0,
2у=4х+5,
у=2х+2,5. Прямая у=2х+2,5 пересекает оси координат в точках (2; 2,5) и
(1,5; 0).
Площадь ΔАОВ равна S=0,5·1,5·2,5=1,875 кв. ед.
2у-4х-5=0,
2у=4х+5,
у=2х+2,5. Прямая у=2х+2,5 пересекает оси координат в точках (2; 2,5) и
(1,5; 0).
Площадь ΔАОВ равна S=0,5·1,5·2,5=1,875 кв. ед.
Приложения:
mruzunov47:
Я допустил опечатку. у=0 ; х=1,25; S=0,5·1,25·2,5=1,5625кв.ед.
Похожие вопросы
Предмет: Английский язык,
автор: fashdj
Предмет: Английский язык,
автор: bbekaa
Предмет: Биология,
автор: vitamsoltysiv
Предмет: Математика,
автор: sasha2993270
Предмет: Литература,
автор: shirkova84