Question

Пожалуйста помогите мне решить эту задачку!

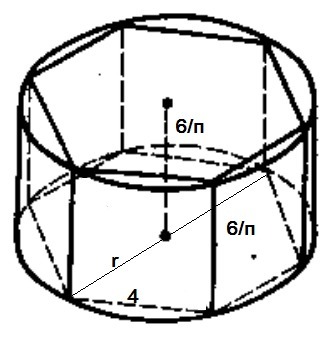
Вокруг прямой призмы, в основании которой лежит правильный шестиугольник со стороной 4, описан цилиндр. Найти объем цилиндра, если боковое ребро призмы равняется 6/π

Answer 1

Vцил=πr²h, где r-радиус основания, h-высота цилиндра.
r основания =r описанной окружности вокруг правильного шестиугольника.
r=a=4
h цилиндра = h призмы=6/π⇒
Vцил=πr²h=π*4²*6/π=96π²≈946,5