Предмет: Математика,
автор: nikita000999
Неопределенный интеграл
Приложения:
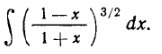
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: amirusmanov010610
Предмет: Информатика,
автор: sarlikondratenko
Предмет: Математика,
автор: danilka2007
Предмет: Математика,
автор: Анастасиянастя111