Предмет: Математика,
автор: nikita000999
Интегрирование иррациональностей.
Приложения:
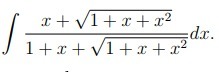
Ответы
Автор ответа:
2
nikita000999:
интеграл от 144/25/t+2,разве это не натуральный логарифм,под дифференциал можно занести двойку,d(t+2)?
Да, конечно, это ln|t+2|, я забыла проинтегрировать эту дробь...
Исправила.
Похожие вопросы
Предмет: История,
автор: alekseevivan2077
Предмет: Математика,
автор: nug2010sansyzbai
Предмет: Геометрия,
автор: makarovans2007
Предмет: Математика,
автор: эмма69
Предмет: Математика,
автор: anushvartanyan1