Предмет: Геометрия,
автор: petya50
Визначите скільки сторін має правильний многокутник у якого внутрішній кут у 8 разів більший за зовнішній
Ответы
Автор ответа:
13
Внешний угол правильного многоугольника и его внутренний угол являются смежными, значит, их сумма равна 180°.
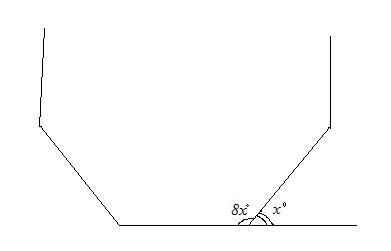
Т.к. по условию задачи внутренний угол в 8 раз больше внешнего, то пусть внешний угол х°, тогда внутренний угол будет равен (8х)° (см. рис.). Составим и решим уравнение:
х + 8х = 180.
9х = 180,
х = 180 : 9,
х = 20.
Значит, внутренний угол правильного многоугольника равен
8 · 20° = 160°.
Внутренний угол правильного многоугольника находят по формуле:
180° · (n - 2) / n, где n - число сторон правильного многоугольника.
Имеем:
180° · (n - 2) / n = 160°,
180° · (n - 2) =160° · n,
9 · (n - 2) = 8 · n,
9n - 18 = 8n,
9n - 8n = 18,
n = 18.
Значит, наш правильный многоугольник имеет 18 сторон.
Ответ: 18 сторон.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: polusikvasilok
Предмет: Другие предметы,
автор: bananov228
Предмет: Математика,
автор: ieva23
Предмет: Математика,
автор: Adlan13