Question

Срочно помогите решить одно задание по геометрии за 35 баллов

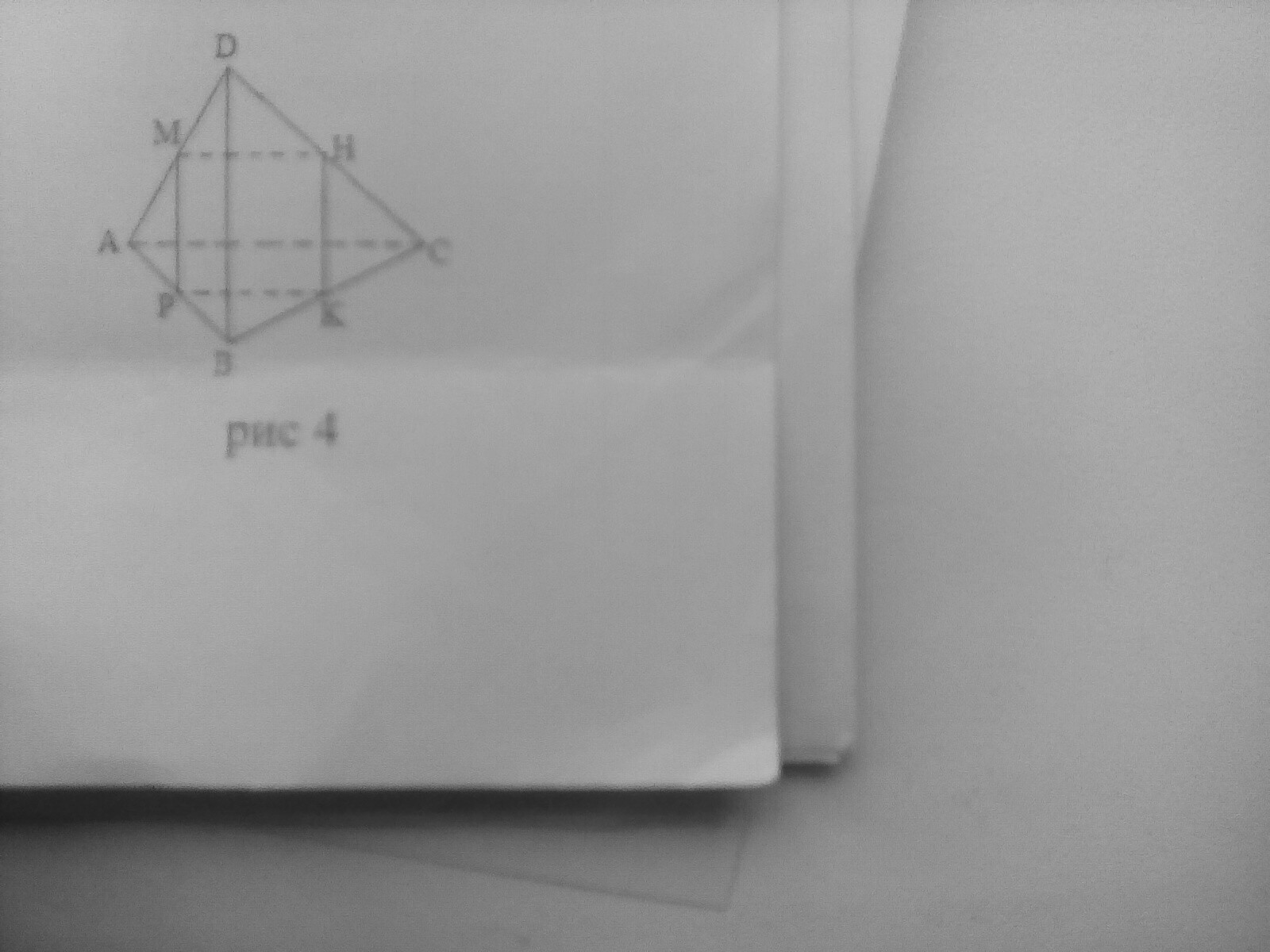
4. M,H,K - середины соответственно сторон AD, DC, CB.
MP II (BCD). AC=10 см, BD=8 см. Периметр четырёхугольника МНКР равен...(рис 4)

Answer 1

Плоскость MHKP пересекает плоскость ΔBDC по линии HK.
HK║BD как средняя линия ΔDCB;  
MP║(BCD)  и MP лежит в плоскости   MHKP   ⇒
 MP║HK   и  MP║BD

MH - средняя линия ΔADC ⇒  MH = 1/2 AC
PK  - средняя линия ΔABC ⇒  PK = 1/2 AC
KH - средняя линия ΔDCB ⇒  HK = 1/2 BD
MP - средняя линия ΔDAB ⇒  MP = 1/2 BD
$P_{MHKP}= MH + PK + KH + MP$ = 
= 1/2 AC + 1/2 AC + 1/2 BD + 1/2 BD = AC + BD =
= 10 см + 8 см = 18 см  
Ответ: периметр MHKP = 18 см