Question

В кругу проведена хорда AB=32 см, которая находится на расстоянии
12 см от центра круга.

1. Радиус круга равен
см;

2. Площадь круга равна

28
256
1024
144
400
πсм2

Answer 1

Ответ:

1) R = 20 см

2) S = 400·π см²

Объяснение:

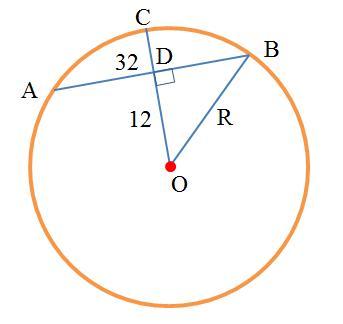
Дано (см. рисунок):

 AB = 32 см - хорда окружности

 OD = 12 см - расстояние от центра круга до АВ

Найти: 1) Радиус R окружности;

            2) Площадь круга.

Решение. Проведём радиус OC перпендикулярный хорде. По свойству радиуса радиус, перпендикулярный хорде, делит эту хорду пополам. Тогда

DB = AB/2 = 32/2 = 16 см.

1) Проведём радиус OB и получаем прямоугольный треугольник ODB с гипотенузой OB=R. По теореме Пифагора в прямоугольном треугольнике ODB:

R² = OD²+DB² = 12²+16² = 144+256 = 400 = 20²

или R = 20 см.

2) Площадь круга S, ограниченный окружностью радиуса R определяется по формуле

S = π·R².

Так как R = 20 см, то

S = π·(20 см)² = 400·π см².