Предмет: Геометрия,
автор: Аноним
НАПИШИТЕ ПОДРОБНО ВСЕ 2 ЗАДАЧИ ,ЕСЛИ НЕ ЗНАЕТЕ НЕ ПИШИТЕ ДОСТАЛИ БАЛЫ КРАСТЬ !!!!!!!1
Приложения:
dnepr1:
Надо было задачи дать отдельно.
Да хоть три! Но по одной ))
Ответы
Автор ответа:
2
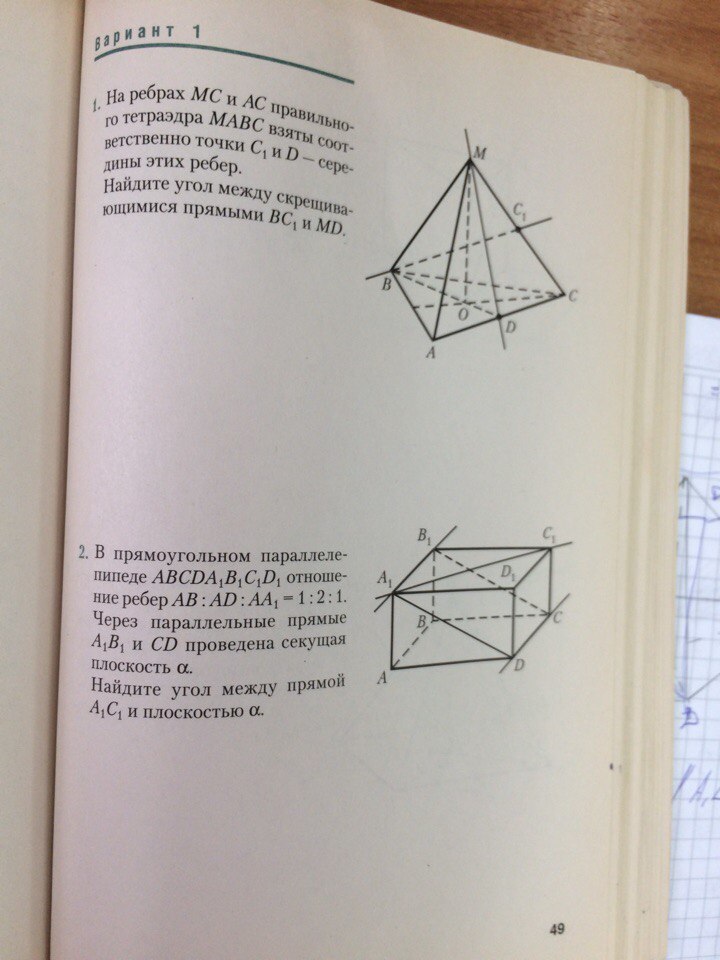
1) У правильного тетраэдра все рёбра равны и все грани - равносторонние треугольники.
Примем длину ребра L = 1.
Медиана каждой грани (в том числе ВД) равна √3/2,
Высота правильного тетраэдра Н = √(2/3).
Поместим тетраэдр в прямоугольную систему координат вершиной В в начало, ВС - по оси Оу.
Определим координаты точек, находящихся на заданных прямых.
В(0; 0; 0), С1((√3/12); 0,75; (√6/6)).
Вектор ВС: ((√3/12); 0,75; (√6/6)). Его модуль равен √3/2.
М(√3/6; 0,5; √(2/3)), Д((√3/4); 0,75; 0).
Вектор МД: ((√3/12); -0,25; (-√2/3)). Его модуль равен √3/2.
Находим скалярное произведение векторов:
ВСхМД = (3/144) + (3/16) - (1/3) = -(1/8) = -0,125.
Косинус угла равен |-0.125|/((√3/2)*(√3/2)) = (1/8)/)3/4) = 1/6.
Угол равен arc cos(1/6) = 1,403348 радиан = 80,40593°.
2) Примем длину рёбер 1, 2 и 1.
Из точки О (середина А1С1) опустим перпендикуляр на плоскость альфа. Пусть это точка Е. Длину ОЕ примем за х.
Проведём сечение через точку О перпендикулярно СД.
Плоскость альфа даст в сечении линию КМ, равную диагонали А1Д боковой грани.
Отрезок КЕ по пропорции равен 2х.
Рассмотрим треугольник КОЕ. КО = 1. По Пифагору 1² = х² + (2х)².
Отсюда х = 1/√5, а КЕ = 2х = 2/√5.
В плоскости верхнего основания определим длину А1О:
А1O = √((1/2)² + 1²) = √(5/4) = √5/2.
Отсюда синус искомого угла β равен:
sin β = x/(A1O) = (1/√5)/(√5/2) = 2/5.
Сам угол равен 0,411517 радиан = 23,57818°.
Примем длину ребра L = 1.
Медиана каждой грани (в том числе ВД) равна √3/2,
Высота правильного тетраэдра Н = √(2/3).
Поместим тетраэдр в прямоугольную систему координат вершиной В в начало, ВС - по оси Оу.
Определим координаты точек, находящихся на заданных прямых.
В(0; 0; 0), С1((√3/12); 0,75; (√6/6)).
Вектор ВС: ((√3/12); 0,75; (√6/6)). Его модуль равен √3/2.
М(√3/6; 0,5; √(2/3)), Д((√3/4); 0,75; 0).
Вектор МД: ((√3/12); -0,25; (-√2/3)). Его модуль равен √3/2.
Находим скалярное произведение векторов:
ВСхМД = (3/144) + (3/16) - (1/3) = -(1/8) = -0,125.
Косинус угла равен |-0.125|/((√3/2)*(√3/2)) = (1/8)/)3/4) = 1/6.
Угол равен arc cos(1/6) = 1,403348 радиан = 80,40593°.
2) Примем длину рёбер 1, 2 и 1.
Из точки О (середина А1С1) опустим перпендикуляр на плоскость альфа. Пусть это точка Е. Длину ОЕ примем за х.
Проведём сечение через точку О перпендикулярно СД.
Плоскость альфа даст в сечении линию КМ, равную диагонали А1Д боковой грани.
Отрезок КЕ по пропорции равен 2х.
Рассмотрим треугольник КОЕ. КО = 1. По Пифагору 1² = х² + (2х)².
Отсюда х = 1/√5, а КЕ = 2х = 2/√5.
В плоскости верхнего основания определим длину А1О:
А1O = √((1/2)² + 1²) = √(5/4) = √5/2.
Отсюда синус искомого угла β равен:
sin β = x/(A1O) = (1/√5)/(√5/2) = 2/5.
Сам угол равен 0,411517 радиан = 23,57818°.
Похожие вопросы
Предмет: Геометрия,
автор: ruouoruru
Предмет: История,
автор: Midibrain
Предмет: Математика,
автор: ismayilovkenan002
Предмет: Математика,
автор: вова323
Предмет: География,
автор: PavelKI567