Предмет: Математика,
автор: Enemy66
Помогите решить задачу по математике!
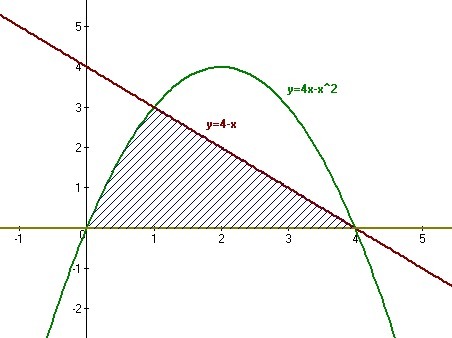
Найти площадь фигуры ограниченной параболой:
у=4x-x2
y=4-x и осью Ох
Приложения:

Ответы
Автор ответа:
2
Приложения:
Enemy66:
А можно еще точки x и y к функциям?
какие именно пересечения графиков?
Нет, построения параболы например x=0 y=1
Парабола: (-1;-5);(0;0);(1;3);(2;4);(3;3);(4;0);(5;-5);
Прямая: (0;4);(1;3);(2;2);(3;1);(4;0)
Прямая: (0;4);(1;3);(2;2);(3;1);(4;0)
Похожие вопросы
Предмет: Английский язык,
автор: natali9788
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: rustim7711
Предмет: Физика,
автор: HAppY967