Question

/Задачка из эстонской олимпиады Кенгуру, 7-8 класс, 5 баллов/

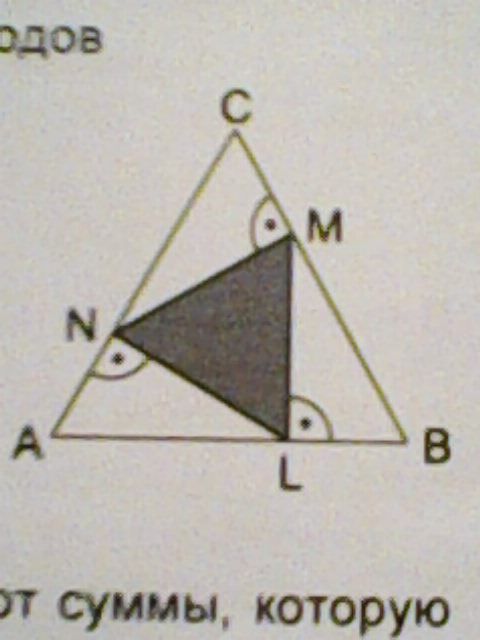
Точки L, M и N лежат на сторонах равностороннего треугольника ABC так, что отрезок ML перпендикулярен стороне AB, NM перпендикулярен стороне BC, а LN перпенликулярен стороне AC. Площадь треугольника ABC равна 36. Найди площадь треугольника LMN.
А: 9 B: 12 C: 15
D: 16 E:18
Желательно с объяснением.

Answer 1

Так как треугольник правильный, то все его углы равны 60°.
Рассмотрим треугольник MLB. Угол LBM=60°, тогда угол BML=30°.
Пусть LB=х. Тогда MB=2х, так как катет, лежащий против угла в 30°, равен половине гипотенузы. По теореме Пифагора найдем ML:
$LM= \sqrt{MB^2-LB^2} =\sqrt{4x^2-x^2} =x \sqrt{3}$
Сторона исходного треугольника равна:
$AB=AL+LB=MB+LB=2x+x=3x$
По построению, треугольник LMN правильный, значит он подобен с треугольником ABC.
Площади подобных треугольников относятся как квадрат коэффициента пропорциональности:
$\dfrac{S_{LMN}}{S_{ABC}} = \left(\dfrac{LM}{AB} \right)^2 \\\ S_{LMN}= \left(\dfrac{LM}{AB} \right)^2 \cdot S_{ABC} \\\ S_{LMN}= \left(\dfrac{x \sqrt{3} }{3x} \right)^2\cdot 36= \dfrac{1}{3} \cdot 36=12$
Ответ: 12