Предмет: Алгебра,
автор: Hiklop
Объясните пожалуйста как решать .....
Приложения:
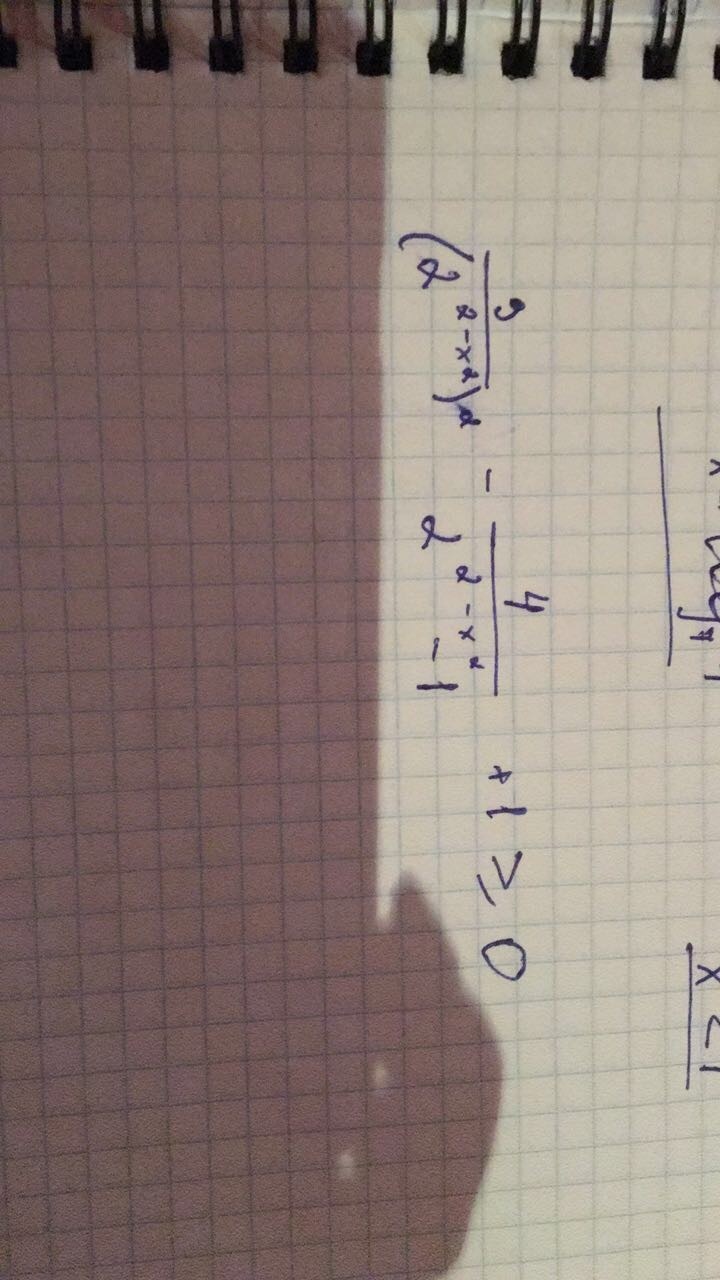
Ответы
Автор ответа:
0
заменой решать))
2 в степени (2-х²) заменить на (а), записав ОДЗ:
2 в степени (2-х²) ≠ 1 ---> x≠-√2; x≠+√2
(2 ни в какой степени никогда не равно нулю...) a>0
дроби сложим (приведем к общему знаменателю):

числитель нужно разложить на множители...
устно проверяем делители свободного члена: 9 кратно {-9;-3;-1;1;3;9}
при а=3: 27-45+27-9=0
т.е. числитель нацело разделится на скобку (а-3)
а³-5а²+9а-9 = (а-3)(а²-2а+3)
для второй скобки D=4-4*3 < 0 ---> корней нет, это парабола, ветви вверх, т.е. во второй скобке никогда не будет отрицательного числа или нуля... а²-2а+3 > 0 всегда (для любых (а))
осталось решить неравенство:
++++++(0)+++++(1)-----[3]+++++ методом интервалов))
вернемся к переменной икс:
2 в степени (2-х²) < 1 или 2 в степени (2-х²) ≥ 3
2-х² < 0 или 2-х² ≥ log₂(3)
х²-2 > 0 или х²+(log₂(3) - 2) ≤ 0
x < -√2 или x > √2 или -√(log₂(⁴/₃)) ≤ x ≤ √(log₂(⁴/₃))
2 в степени (2-х²) заменить на (а), записав ОДЗ:
2 в степени (2-х²) ≠ 1 ---> x≠-√2; x≠+√2
(2 ни в какой степени никогда не равно нулю...) a>0
дроби сложим (приведем к общему знаменателю):
числитель нужно разложить на множители...
устно проверяем делители свободного члена: 9 кратно {-9;-3;-1;1;3;9}
при а=3: 27-45+27-9=0
т.е. числитель нацело разделится на скобку (а-3)
а³-5а²+9а-9 = (а-3)(а²-2а+3)
для второй скобки D=4-4*3 < 0 ---> корней нет, это парабола, ветви вверх, т.е. во второй скобке никогда не будет отрицательного числа или нуля... а²-2а+3 > 0 всегда (для любых (а))
осталось решить неравенство:
++++++(0)+++++(1)-----[3]+++++ методом интервалов))
вернемся к переменной икс:
2 в степени (2-х²) < 1 или 2 в степени (2-х²) ≥ 3
2-х² < 0 или 2-х² ≥ log₂(3)
х²-2 > 0 или х²+(log₂(3) - 2) ≤ 0
x < -√2 или x > √2 или -√(log₂(⁴/₃)) ≤ x ≤ √(log₂(⁴/₃))
Похожие вопросы
Предмет: Математика,
автор: rdaniil2009
Предмет: Математика,
автор: Texno28273
Предмет: Литература,
автор: garlicdanil0108
Предмет: Алгебра,
автор: Kekyshka34
Предмет: Математика,
автор: Osmanlo