Предмет: Алгебра,
автор: polyamigneva
Решите логарифмическое неравенство
Приложения:
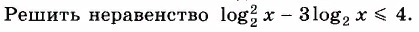
Ответы
Автор ответа:
1
Область допустимых значений аргумента: х>0.
Сделаем замену: log2(х)=а, получим
а²-3а≤4 перенесём вправо четвёрку
а²-3а-4≤0 решим
(а-4)(а+1)≤0, то есть решением будут значения а∈[-1;4].
Делаем обратную замену и получим
-1≤log2(х)≤4 прологарифмируем
log2(1/2)≤log2(х)≤log2(16) поскольку основание 2>1, то
1/2≤х≤16. Из этих решений ОДЗ удовлетворяют все.
Ответ: х∈[0,5;16].
Сделаем замену: log2(х)=а, получим
а²-3а≤4 перенесём вправо четвёрку
а²-3а-4≤0 решим
(а-4)(а+1)≤0, то есть решением будут значения а∈[-1;4].
Делаем обратную замену и получим
-1≤log2(х)≤4 прологарифмируем
log2(1/2)≤log2(х)≤log2(16) поскольку основание 2>1, то
1/2≤х≤16. Из этих решений ОДЗ удовлетворяют все.
Ответ: х∈[0,5;16].
Похожие вопросы
Предмет: Русский язык,
автор: takeabook58
Предмет: Физика,
автор: hhgghg
Предмет: Алгебра,
автор: lizalisa2000yevseeva
Предмет: Математика,
автор: Нитик1