Question

Даю 40 баллов, умоляю.
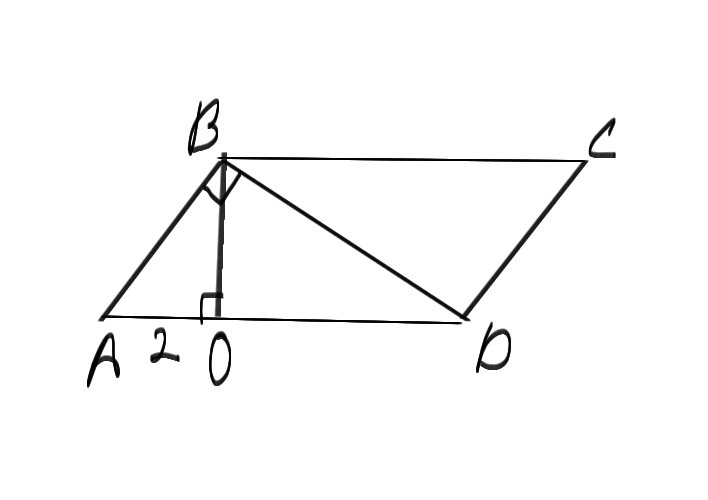
В параллелограмме АBCD диагональ BD перпендикулярна стороне AB,отрезок BO-высота, проведенная из вершины В. Вычислите площадь параллелограмма, если АО=2 см, АB:AD=1:2.

Answer 1

ΔABO подобен ΔABD (∠ABD=90°=∠AOB, ∠A - общий)
$\frac{AB}{AD} = \frac{BO}{BD}= \frac{AO}{AB} = \frac{1}{2} \\ \frac{AO}{AB}= \frac{1}{2}; \frac{2}{AB}= \frac{1}{2} ; AB=4$
$\frac{AB}{AD}= \frac{1}{2}; \frac{4}{AD} = \frac{1}{2}; AD= 8$. По т.Пифагора: BD=$\sqrt{ AD^{2}- AB^{2} } = \sqrt{64-16} = \sqrt{48} \\ Sabcd=AB*BD=4 \sqrt{48} =8 \sqrt{12}$