До завтра, срочно помогите

Ответы
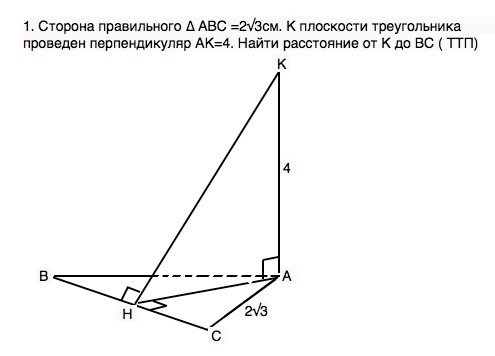
1. Сторона правильного ∆ АВС =2√3 см. К плоскости треугольника проведен перпендикуляр АК=4. Найти расстояние от К до ВС ( ТТП)
Расстояние от точки до прямой измеряется длиной отрезка, проведенного из точки к прямой перпендикуляно.
АН - высота ∆ АВС. АН⊥ВС.
КН⊥ВС по т. о 3-х перпендикулярах.
КН - искомое расстояние.
AH=AC•sin60°=2√3•√3/2=3
По т.Пифагора КН=√(AK²+AH²)=√(16+9)=5.
––––––––––––––––––––––––
2.Концы отрезка лежат в двух взаимно перпендикулярных плоскостях. Проекции отрезка на плоскостях 20 см и 16 см. Расстояние между основаниями перпендикуляров, проведенных из концов отрезка к линии пересечения плоскостей 12 см. Длина отрезка?
———
Обозначим отрезок АВ. Т.А лежит в плоскости β, точка В в плоскости α. m- линия пересечения плоскостей.
АС – перпендикуляр к m.
СВ - проекция АВ на плоскость α.
ВН - перпендикуляр к m,
АН - проекция ВА на плоскость β.
СН- расстояние между основаниями перпендикуляров на линии m.
∆ СНВ прямоугольный, СВ - гипотенуза.
По т.Пифагора ВН²=BC²-CH²=16²
Из прямоугольного ∆ АНВ по т.Пифагора
АВ=√(AH²+BH²)=√(16²+16²)=16√2 см