Предмет: Геометрия,
автор: demonova86
Помогите пожалуйста, геометрия с рисунком. На украинсом желательно)
Основою правильної призми AA1B1BCC1 є трикутник ABC. т.К- середина ребра BC. Площина, що проходить через точки AKB1-утворює з площиною основи призми куть a( альфа), визначте V призми, якщо відстань від вершини a до грані BB1C1C=d.
Ответы
Автор ответа:
26
Так як основа ПРАВИЛЬНА, отже основою призми є ПРАВИЛЬНИЙ ТРИКУТНИК ABC.
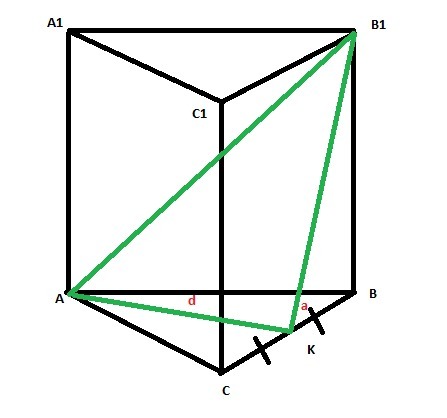
Зеленим кольором позначив площину.
Оскільки призма ПРАВИЛЬНА то BB1⊥ (ABC), тому (ABC)⊥(BB1C1) за ознакою перпендикулярності площин.т.A∈(ABC), тому за властивістю перпендикулярних площин р(A;(BB1C1)) , AK=d, бо AK⊥BC, як медіана і висота рівностор. трикутника.
B1K- похила, BK- проекція на (ABC), BK⊥AK, бо BC⊥AC, тому за ТТП B1K⊥AK, AK-лінія перетину (ABC)∩(AB1K). Тоді за означенням кута між площинами ∠B1KB=a.
Vпризми-?
Vпр=S(основи)*h=S(abc)*BB1=
BC-? BB1-?
Відомо, що AK=BC√3/2. d=BC√3/2⇒BC√3=2d⇒2d/√3
ЗΔB1BK (∠BB1K=90°) BB1=BK*tgB1KB⇒BB1=1/2BC*tga⇒B1B=1/2*2d/√3*tg(a)=tg(a)/√3
Отже V призми=(2d/√3)²√3*d√3*tg(a)/4*√3=
Відповідь:
Зеленим кольором позначив площину.
Оскільки призма ПРАВИЛЬНА то BB1⊥ (ABC), тому (ABC)⊥(BB1C1) за ознакою перпендикулярності площин.т.A∈(ABC), тому за властивістю перпендикулярних площин р(A;(BB1C1)) , AK=d, бо AK⊥BC, як медіана і висота рівностор. трикутника.
B1K- похила, BK- проекція на (ABC), BK⊥AK, бо BC⊥AC, тому за ТТП B1K⊥AK, AK-лінія перетину (ABC)∩(AB1K). Тоді за означенням кута між площинами ∠B1KB=a.
Vпризми-?
Vпр=S(основи)*h=S(abc)*BB1=
BC-? BB1-?
Відомо, що AK=BC√3/2. d=BC√3/2⇒BC√3=2d⇒2d/√3
ЗΔB1BK (∠BB1K=90°) BB1=BK*tgB1KB⇒BB1=1/2BC*tga⇒B1B=1/2*2d/√3*tg(a)=tg(a)/√3
Отже V призми=(2d/√3)²√3*d√3*tg(a)/4*√3=
Відповідь:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: viktoriapancosak
Предмет: Физика,
автор: ninsanofa
Предмет: Алгебра,
автор: perfectym555
Предмет: Алгебра,
автор: махито3