Предмет: Математика,
автор: ElzaSnowWhite
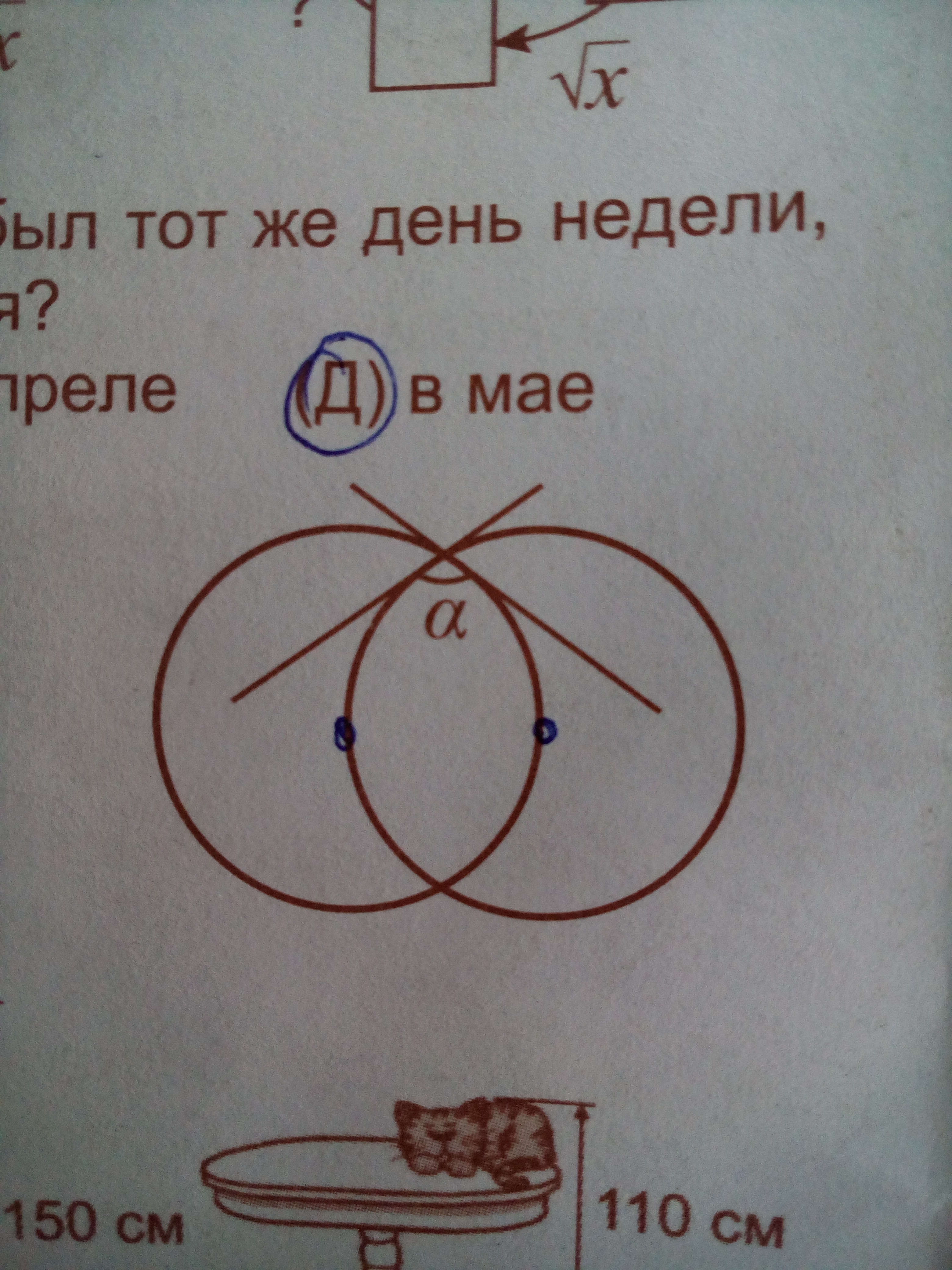
Окружности на рисунке имеют одинаковый радиус и проходят через центры друг друга. В точке пересечения к ним провели касательные. Чему равен угол а?
Приложения:
Ответы
Автор ответа:
1
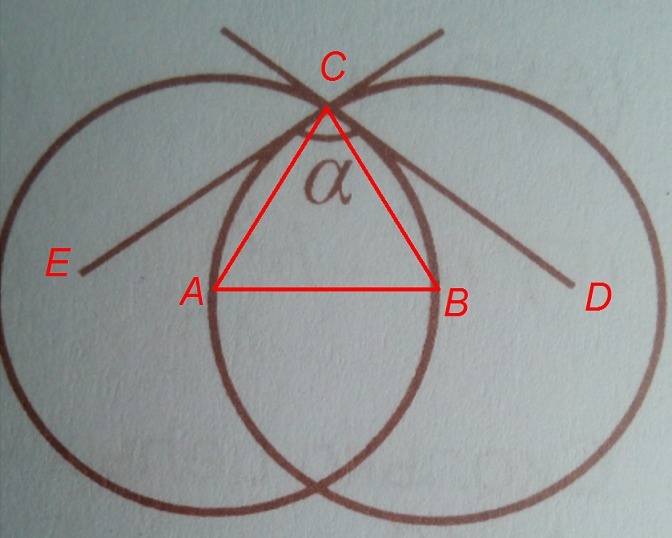
Соединим
центры окружностей их общим радиусом. Также соединим центры окружностей с
точкой касания радиусами. Образовался равносторонний треугольник АВС.
Радиус АС, проведенный в точку касания, перпендикулярен касательной CD. Значит, угол АСD - прямой. Учитывая, что угол АСВ - угол равностороннего треугольника, равный 60°, получим, что угол ВСD равен 30°.
Аналогично, получим, что угол АСЕ равен 30°.
Тогда искомый угол α равен сумме углов АСЕ, АСВ и ВСD:
α=30°+60°+30°=120°
Ответ: 120°
Радиус АС, проведенный в точку касания, перпендикулярен касательной CD. Значит, угол АСD - прямой. Учитывая, что угол АСВ - угол равностороннего треугольника, равный 60°, получим, что угол ВСD равен 30°.
Аналогично, получим, что угол АСЕ равен 30°.
Тогда искомый угол α равен сумме углов АСЕ, АСВ и ВСD:
α=30°+60°+30°=120°
Ответ: 120°
Приложения:
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Обществознание,
автор: vladger456
Предмет: Другие предметы,
автор: polina129000
Предмет: Химия,
автор: andry16
Предмет: Алгебра,
автор: диана700