Question

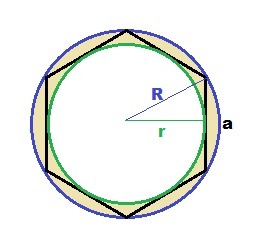
Cторона правильного шестиугольника равна 4 корня из 3 найдите площадь кольца между окружностями одна из которых описана около этого шестиугольника другая вписана в него.
Нужно с решением.
Выберите ответ.
1.11П
2.8П
3.10П
4.12П
5.13П

Answer 1

Cторона правильного шестиугольника  а = 4√3.
Радиус описанной около шестиугольника окружности
R = a = 4√3.
Радиус вписанной в шестиугольник окружности
r = a * √3/2 = 4√3 * √3/2 = 6
Площадь кольца - это площадь описанного круга минус площадь вписанного круга.
S = S₀ - S₆ = πR² - πr² = π( (4√3)² - 6² ) = π (48-36) = 12π

Ответ: 4) 12π