Предмет: Геометрия,
автор: Flashbrz
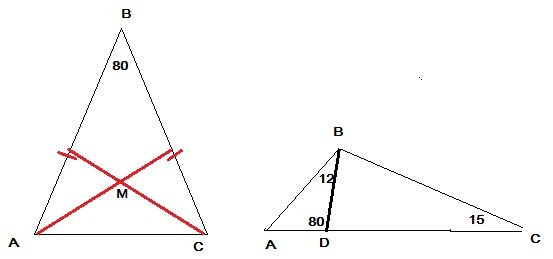
1. В треугольнике АВС АВ=ВС, угол В равен 80 градусов. Биссектрисы углов А и С пересекаются в точке М. Найдите угол АМС.
2. В треугольнике АВС угол С равен 15 градусов. На стороне АС отмечена точка D так, что угол АВD равен 12 градусов, угол ADB равен 80 градусов. Докажите, что треугольник АВС не является прямоугольным.
Ответы
Автор ответа:
12
1. ∠А=∠С=(180-80)/2=50°
∠МАС=∠МСА=25°, так как АМ, МС- биссектрисы по условию.⇒
∠АМС=180-2*25=130°
2. В ΔАDВ ∠А=180-∠АВD-∠АDВ=180-80-12=88°
В ΔАВС ∠В=180-∠А-∠С=180-88-15=77°⇒
в ΔАВС нет углов, равных 90°⇒ΔАВС не прямоугольный,
что и требовалось доказать.
∠МАС=∠МСА=25°, так как АМ, МС- биссектрисы по условию.⇒
∠АМС=180-2*25=130°
2. В ΔАDВ ∠А=180-∠АВD-∠АDВ=180-80-12=88°
В ΔАВС ∠В=180-∠А-∠С=180-88-15=77°⇒
в ΔАВС нет углов, равных 90°⇒ΔАВС не прямоугольный,
что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kapanovnazupar
Предмет: Английский язык,
автор: uwus12312
Предмет: Русский язык,
автор: mila309300
Предмет: Литература,
автор: Танюха111111
Предмет: Физика,
автор: dachad651