Предмет: Математика,
автор: Shanon
Решить неопределенный интеграл
Приложения:
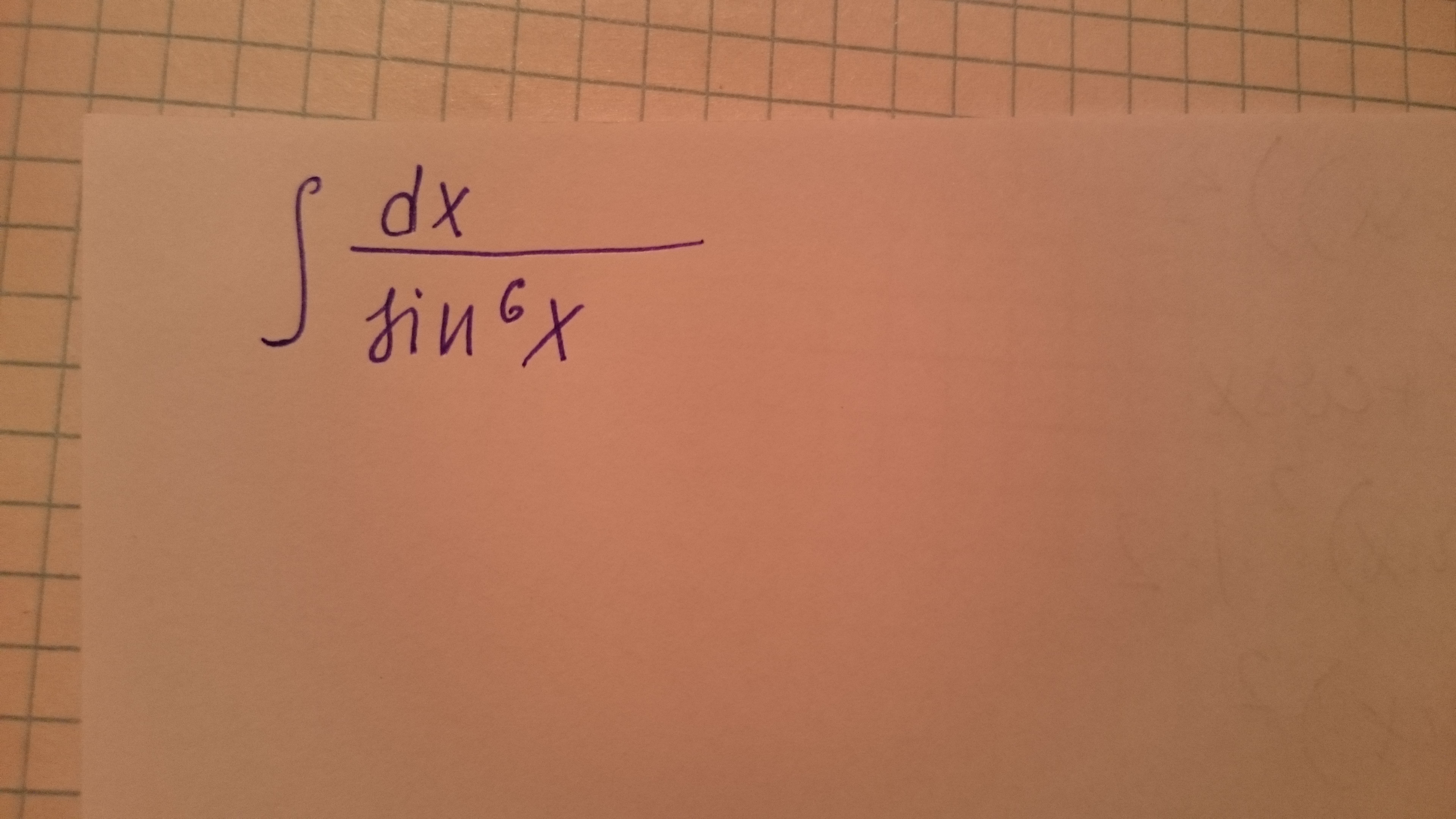
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: wer123578
Предмет: Химия,
автор: yulia13690
Предмет: География,
автор: pivoputina
Предмет: Алгебра,
автор: АНТО14
Предмет: Математика,
автор: LubSmillon3duS