Предмет: Алгебра,
автор: Alena2004567
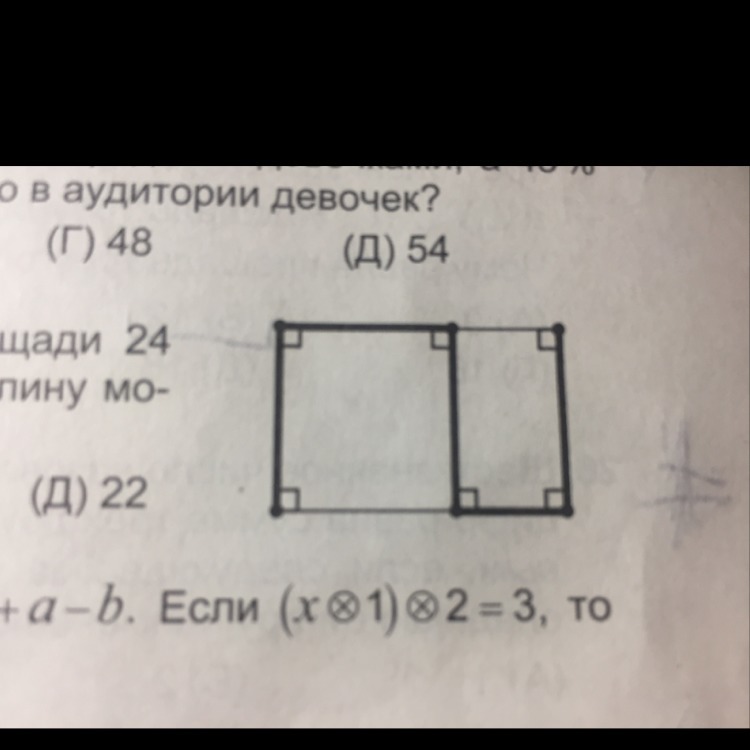
На рисунке изображён прямоугольник площади 24 с целыми сторонами. Какую наименьшую длину может иметь ломаная на рисунке? А)12). Б)16. В)17. Г)18. Д)22
Приложения:
Ответы
Автор ответа:
10
Длина ломаной а рисунке равна сумме длины прямоугольника и его утроенной ширины:
l=x+3y
Рассмотри различные разложения числа 24 на натуральные множители:
24=24·1, l=x+3y=24+3·1=27
24=12·2, l=x+3y=12+3·2=18
24=8·3, l=x+3y=8+3·3=17
24=6·4, l=x+3y=6+3·4=18
Далее результат будет только увеличиваться, поскольку увеличивается ширина, а она входит в искомую сумму три раза.
Наименьший результат 17.
Ответ: 17
l=x+3y
Рассмотри различные разложения числа 24 на натуральные множители:
24=24·1, l=x+3y=24+3·1=27
24=12·2, l=x+3y=12+3·2=18
24=8·3, l=x+3y=8+3·3=17
24=6·4, l=x+3y=6+3·4=18
Далее результат будет только увеличиваться, поскольку увеличивается ширина, а она входит в искомую сумму три раза.
Наименьший результат 17.
Ответ: 17
Похожие вопросы
Предмет: Математика,
автор: evasalovej
Предмет: Алгебра,
автор: Nadyusha150
Предмет: Химия,
автор: lovsonix
Предмет: Алгебра,
автор: 02bychok
Предмет: Алгебра,
автор: irekminikaev